题目内容
12．
如图，AB是圆O的直径，点C在圆O上，若∠A=40°，则∠B的度数为50°．
分析 根据圆周角定理得到∠ACB=90°，然后根据三角形内角和定理计算∠ABC的度数．
解答 解：∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠B=90°-∠A=90°-40°=50°，
故答案为50°．
点评 本题考查了圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径是解答此题的关键．
练习册系列答案
相关题目
2．
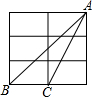如图是一个3×2的长方形网格，组成网格的小长方形长为宽的2倍，△ABC的顶点都是网格中的格点，则cos∠ABC的值是（ ）
如图是一个3×2的长方形网格，组成网格的小长方形长为宽的2倍，△ABC的顶点都是网格中的格点，则cos∠ABC的值是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
如图，⊙O是正方形ABCD的外接圆，点P在⊙O上，则∠APB=45°．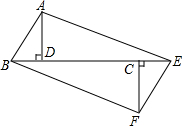
如图，已知△ABD和△CEF都是斜边为2cm的全等直角三角形，其中∠ABD=∠FEC=60°，且B、D、C、E都在同一直线上，DC=4．
17．$-\frac{1}{2016}$的绝对值是（ ）
| A． | $-\frac{1}{2016}$ | B． | $\frac{1}{2016}$ | C． | 2016 | D． | -2016 |
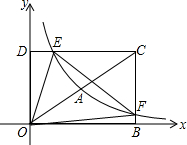如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）．若反比例函数$y=\frac{k}{x}$（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F．设直线EF的解析式为y=mx+n．
1．下列运算正确的是（ ）
| A． | （a-b）2=a2-b2 | B． | -2x2+x2=-3x2 | C． | $\sqrt{（-2）^{2}}$=-2 | D． | a2•a3=a5 |