题目内容
11.分式方程$\frac{x}{x-1}=\frac{2}{3x-3}$的解为x=$\frac{2}{3}$.分析 方程两边都乘以3(x-1)化为整式方程,然后求解,再检验即可.
解答 解:方程两边都乘以3(x-1)得,
3x=2,
解得x=$\frac{2}{3}$,
检验:当x=$\frac{2}{3}$时,3(x-1)=3(1-$\frac{2}{3}$)=1≠0,
所以,x=$\frac{2}{3}$是方程的解,
所以,原分式方程的解是x=$\frac{2}{3}$.
故答案为:x=$\frac{2}{3}$.
点评 本题考查了解分式方程,(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
2.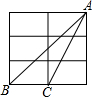 如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )
如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )
 如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )
如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
16.$\frac{22}{7}$是( )
| A. | 整数 | B. | 自然数 | C. | 无理数 | D. | 有理数 |
1.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | -2x2+x2=-3x2 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | a2•a3=a5 |
 如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A、B两点,当k=2时;
如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A、B两点,当k=2时; 如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB=45°.
如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB=45°.