题目内容
12.2016年5月29日,北京园博园迎来了“挑战100,一起跑”百公里接力路跑赛事,活动里程共100公里,采用10人×10公里的方式展开接力竞赛.王刚是一名长跑爱好者,原来每天从家匀速跑步到单位,共12公里.为参加此次活动,王刚计划加强训练,速度提高到原来的1.2倍,结果提前10分钟到单位.问王刚原来每小时跑多少公里?分析 先由题意得出等量关系列出方程即$\frac{12}{x}-\frac{12}{1.2x}=10$,然后解出来,最后检验并作答.
解答 解:设这个人从甲地到乙地原定的平均速度是每分钟x千米,
则根据题意列出方程:$\frac{12}{x}-\frac{12}{1.2x}=10$,解得:x=0.2(千米/分钟),
经检验x=0.2是所列出的分式方程的解,
0.2×60=12
答:王刚原来每小时跑12公里.
点评 本题主要考查分式方程的应用,找到关键描述语,找到合适的等量关系是解决问题的关键.注意:求出的结果必须检验.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
14.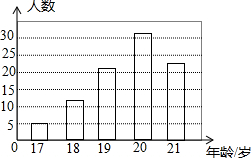 在6月26日“国际禁毒日”来临之际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
在6月26日“国际禁毒日”来临之际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
 在6月26日“国际禁毒日”来临之际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
在6月26日“国际禁毒日”来临之际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
17. 如图,在平面直角坐标系中有△ABC,以点O为位似中心,相似比为2,将△ABC放大,则它的对应顶点的坐标为( )
如图,在平面直角坐标系中有△ABC,以点O为位似中心,相似比为2,将△ABC放大,则它的对应顶点的坐标为( )
 如图,在平面直角坐标系中有△ABC,以点O为位似中心,相似比为2,将△ABC放大,则它的对应顶点的坐标为( )
如图,在平面直角坐标系中有△ABC,以点O为位似中心,相似比为2,将△ABC放大,则它的对应顶点的坐标为( )| A. | (2,$\frac{3}{2}$),($\frac{3}{2},\frac{1}{2}$),($\frac{1}{2},1$) | B. | (8,6)(6,2)(2,4) | ||
| C. | (8,6)(6,2)(2,4)或(-8,-6)(-6,-2)(-2,-4) | D. | (8,-6)(6,-2)(2,-4)或(-8,6)(-6,2)(-2,4) |
4. 如图,在平面直角坐标系中,以原点为位似中心,将线段CD放大得到线段AB,若点B、C、D的坐标分别为B(5,0)、C(1,2)、D(2,0),则点A的坐标是( )
如图,在平面直角坐标系中,以原点为位似中心,将线段CD放大得到线段AB,若点B、C、D的坐标分别为B(5,0)、C(1,2)、D(2,0),则点A的坐标是( )
 如图,在平面直角坐标系中,以原点为位似中心,将线段CD放大得到线段AB,若点B、C、D的坐标分别为B(5,0)、C(1,2)、D(2,0),则点A的坐标是( )
如图,在平面直角坐标系中,以原点为位似中心,将线段CD放大得到线段AB,若点B、C、D的坐标分别为B(5,0)、C(1,2)、D(2,0),则点A的坐标是( )| A. | (2.5,5) | B. | (2.5,3) | C. | (3,5) | D. | (2.5,4) |
2.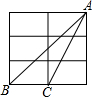 如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )
如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )
 如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )
如图是一个3×2的长方形网格,组成网格的小长方形长为宽的2倍,△ABC的顶点都是网格中的格点,则cos∠ABC的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
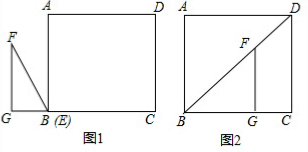
 已知:线段c,直线l及l外一点A.
已知:线段c,直线l及l外一点A.