题目内容
如图,如果将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中四边形ACED的面积为_____.
15
【解析】试题分析：：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．
试题解析：设点A到BC的距离为h，则S△ABC=BC•h=5，
∵平移的距离是BC的长的2倍，
∴AD=2BC，CE=BC，
∴四边形ACED的面积=（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×5=15...
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案直线y=kx+b与抛物线y=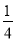
x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为_______________________．
（0，4）
【解析】【解析】
∵直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，∴kx+b=，
化简，得 x2﹣4kx﹣4b=0，∴x1+x2=4k，x1x2=﹣4b．
又∵OA⊥OB，∴ ，
解得，b=4，即直线y=kx+4，故直线恒过顶点（0，4）．
故答案为：（0，4）． 从标号分别为1，2，3，4，5的5张卡片中，随机抽取1张．下列事件中，必然事件是（ ）
A. 标号小于6 B. 标号大于6 C. 标号是奇数 D. 标号是3
A
【解析】试题分析：标号小于6是必然事件，标号大于6是不可能事件，标号是奇数是是随机事件，标号是3的事件是随机事件.
故选：A 如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝12cm，点P是AB边上的一个动点，过点P作PE⊥BC，PF⊥AC.当PB＝_________时，四边形PECF的面积最大，最大值为_______．
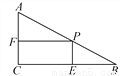
6cm 9cm2
【解析】利用锐角三角函数关系，设PB=xcm，由∠C=90°，∠B=30°，AB=12cm，可得BC=AB×cos30°=6（cm），PE=xcm，BE=xcm，则EC=（6-x）cm，故四边形FCEP的面积为：PE×EC=x×（6-x）=-x2+3x=-（x2-12x）=-（x-6）2+9，故当x=6时，四边形PECF的面积最大，最大值为9．
故答案为：6，9． 对数轴上的点P进行如下操作：先把点P表示的数乘以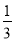
，再把所得数对应的点向右平移1个单位，得到点P的对应点P′，点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′，如图，若点A表示的数是﹣3，则点A′表示的数是__；若点B′表示的数是2，则点B表示的数是__．已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合，则点E表示的数是__．
0 3 1.5
【解析】试题分析：根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B表示的数为a，根据题意列出方程求解即可得到点B表示的数，设点E表示的数为b，根据题意列出方程计算即可得解．
试题解析：【解析】
点A′：﹣3×+1=﹣1+1=0．
设点B表示的数为a，则a+1=2，解得a=3．
设点E表示的数为b，则b+1=b，解得b=1.5．
故答... 关于这一图案，下列说法正确的是（ ）
A. 图案乙是由甲绕BC的中点旋转180°得到的
B. 图案乙是由甲绕点C旋转108°得到的
C. 图案乙是由甲沿AB方向平移3个边长的距离得到的
D. 图案乙是由甲沿直线BC翻转180°得到的
A
【解析】【解析】
如图所示：可得图案乙是由甲绕BC的中点旋转180°得到的．故选A． 如图，△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．由一个三角形变换到另一个三角形（ ）
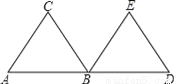
A. 仅能由平移得到
B. 仅能由旋转得到
C. 既能由平移得到，也能由旋转得到
D. 既不能由平移得到，也不能由旋转得到
C
【解析】【解析】
∵△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．
∴这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的．故选C． 已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1）、P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且﹣1＜x1＜x2，x3＜﹣1，则y1、y2、y3的大小关系为（ ）
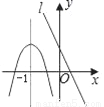
A. y1＜y2＜y3 B. y3＜y1＜y2 C. y3＜y2＜y1 D. y2＜y1＜y3
D
【解析】解析：对称轴为直线x=﹣1，且﹣1＜x1＜x2，当x＞﹣1时，y2＜y1，
又因为x3＜﹣1，由一次函数的图象可知，此时点P3（x3，y3）在二次函数图象上方，
所以y2＜y1＜y3．
故选：D． 已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A，则此三角形（ ）
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
C
【解析】试题解析：∵∠A+∠B+∠C=180°，∠B+∠C=∠A，
∴2∠A=180°，
∴∠A=90°，
即△ABC一定是直角三角形；
故选C．