题目内容
对数轴上的点P进行如下操作：先把点P表示的数乘以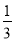
，再把所得数对应的点向右平移1个单位，得到点P的对应点P′，点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′，如图，若点A表示的数是﹣3，则点A′表示的数是__；若点B′表示的数是2，则点B表示的数是__．已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合，则点E表示的数是__．
0 3 1.5
【解析】试题分析：根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B表示的数为a，根据题意列出方程求解即可得到点B表示的数，设点E表示的数为b，根据题意列出方程计算即可得解．
试题解析：【解析】
点A′：﹣3×+1=﹣1+1=0．
设点B表示的数为a，则a+1=2，解得a=3．
设点E表示的数为b，则b+1=b，解得b=1.5．
故答...
某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．
（1）求y与x之间的函数关系式；
（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？
（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？
（1）y=﹣30x+2100．（2）每件售价定为55元时，每星期的销售利润最大，最大利润6750元．
（3）每星期至少要销售该款童装360件．
【解析】试题分析：（1）根据售量y（件）与售价x（元/件）之间的函数关系即可得到结论．
（2））设每星期利润为W元，构建二次函数利用二次函数性质解决问题．
（3）列出不等式先求出售价的范围，再确定销售数量即可解决问题．
试题解... 袋中有5个红球，6个白球，12个黑球，每个球除颜色外都相同，事先选定一种颜色，若摸到的球的颜色与事先选定的一样，则获胜，否则就失败，为了尽可能获胜，你事先应选择的颜色是__．
黑色
【解析】先分别求出摸到红球，白球，黑球的概率，再比较它们的大小，概率最大的即为所求．
【解析】
∵袋中有5个红球，6个白球，12个黑球，
∴袋中一共有球：5+6+12=23（个），
∴摸到红球的概率为： ，
摸到白球的概率为： ，
摸到黑球的概率为： ，
又∵＜＜，
∴摸到黑球的概率最大，会尽可能获胜．
故答案为黑球． 某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形．其中，抽屉底面周长为180cm，高为20cm．请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？（材质及其厚度等暂忽略不计）．
当抽屉底面宽为45cm时，抽屉的体积最大，最大体积为40500cm3
【解析】【解析】
已知抽屉底面宽为x cm，则底面长为180÷2－x=（90－x）cm．
由题意得：。
∴当x=45时，y有最大值，最大值为40500。
答：当抽屉底面宽为45cm时，抽屉的体积最大，最大体积为40500cm3。
根据题意列出二次函数关系式，然后利用二次函数的性质求最大值。
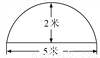
... 如图为某菜农搭建的一个横截面为抛物线的大棚，有关尺寸如图所示，某菜农身高1.6米，则他在不弯腰的情况下在大棚内左右活动的范围是( )
A.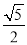 
米 B.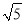 
米 C. 1.6米 D. 0.8米
B
【解析】如图，设抛物线的解析式为y=a（x-2.5）2+2，由待定系数法求出抛物线的解析式y=- （x-2.5）2+2，将y=1.6时代入解析式得- （x-2.5）2+2=1.6，解得， ，他在不弯腰的情况下在大棚里活动的范围是：x1-x2=．
故选：B. 如图,如果将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中四边形ACED的面积为_____.
15
【解析】试题分析：：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．
试题解析：设点A到BC的距离为h，则S△ABC=BC•h=5，
∵平移的距离是BC的长的2倍，
∴AD=2BC，CE=BC，
∴四边形ACED的面积=（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×5=15... 在平面直角坐标系中，线段OP的两个端点坐标分别为O（0，0），P（4， 3），将线段OP绕点O逆时针旋转90°到OP′位置，则点P′的坐标是（ ）
A．（3，4） B．（－4，3） C．（－3，4） D．（4，－3）
C．
【解析】
试题分析：如图，OA=3，PA=4，
把线段OP绕点O逆时针旋转90°到OP′位置可得OA旋转到x轴负半轴OA′的位置，OB旋转到y轴正半轴OB′的位置,所以P′A′=PA=4，P′B′=PB=3,即可得P′点的坐标为（﹣3，4）．故答案选C． 二次函数y=x2+bx+c的图象经过点（4，3），（3，0）．
（1）求b、c的值；
（2）求该二次函数图象的顶点坐标和对称轴．
（1） ；（2）顶点坐标为（2，﹣1），对称轴为直线x=2
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式.
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴ ，
解得 ；
（2）∵该二次函数为y=x2﹣4x+3=（x... 如果△ABC中，两边a＝7cm，b＝3cm，则c的取值范围是_________；第三边为奇数的所有可能值为_________；周长为偶数的所有可能值为_________．
4cm＜c＜10cm 5cm、7cm、9cm 16cm或18cm
【解析】根据三角形的三边关系，得7cm?3cm