题目内容
已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A，则此三角形（ ）
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
C
【解析】试题解析：∵∠A+∠B+∠C=180°，∠B+∠C=∠A，
∴2∠A=180°，
∴∠A=90°，
即△ABC一定是直角三角形；
故选C．
练习册系列答案
相关题目
如图,如果将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中四边形ACED的面积为_____.
15
【解析】试题分析：：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．
试题解析：设点A到BC的距离为h，则S△ABC=BC•h=5，
∵平移的距离是BC的长的2倍，
∴AD=2BC，CE=BC，
∴四边形ACED的面积=（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×5=15... 如图，在△ABC中，AB=AC，BF=CD，BD=CE，∠FDE=α，探索α与∠B的关系。
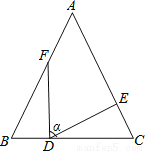
∠α=∠B，理由见解析
【解析】试题分析：根据已知条件易证△BFD≌△CDE，得出∠BFD=∠CDE，再由角之间的转化，进而可得出结论．
【解析过程】
试题解析：
∠α=∠B，理由为：
证明：∵AB=AC（已知），
∴∠B=∠C（等边对等角），
在△BDF和△CED中，
∴△BDF≌△CED（SAS），
∴∠BFD=∠CDE（全等三角形对应角相... 如图，△ABC中，∠C＝90°，CD⊥AB，CM平分AB，CE平分∠DCM，则∠ACE的度数是______．
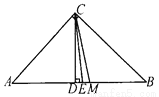
45°
【解析】∵△ABC中,∠C=90°，
∴∠A+∠B=90°，
∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠ACD=∠B，
∵CM平分AB，
∴AM=BM=CM，
∴∠BCM=∠B，
∴∠BCM=∠ACD，
∵CE平分∠DCM，
∴∠DCE=∠MCE，
∴∠ACD+∠DCE=∠BCM+∠M... 如果△ABC中，两边a＝7cm，b＝3cm，则c的取值范围是_________；第三边为奇数的所有可能值为_________；周长为偶数的所有可能值为_________．
4cm＜c＜10cm 5cm、7cm、9cm 16cm或18cm
【解析】根据三角形的三边关系，得7cm?3cm一个钝角三角形的三条角平分线所在的直线一定交于一点，这交点一定在( )
A. 三角形内部 B. 三角形的一边上 C. 三角形外部 D. 三角形的某个顶点上
A
【解析】三角形三条角平分线所在的直线一定交于一点，这一点是三角形的内心即内切圆的圆心，此点在三角形（锐角三角形、直角三角形、钝角三角形）内部.
故选：A. 已知|x﹣y+2|+
=0，则x2﹣y2的值为______．
﹣4
【解析】因为|x?y+2|+=0，∴x?y+2=0，x+y?2=0，
∴x?y=?2，x+y=2，∴x²?y²=(x?y)(x+y)=?4.
故答案为：?4. 已知抛物线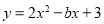
的对称轴是直线
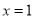，则
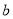的值为 ．
b=4
【解析】
试题分析：由抛物线的对称轴x=-和已知条件抛物线y=2-bx+3的对称轴是直线x=1，得到的等式，即可求出b的值． 如图，直线y=x+b与直线y=kx+6交于点P（3，5），则关于x的不等式x+b＞kx+6的解集是_____．
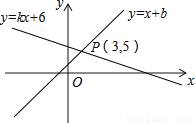
x＞3.
【解析】试题解析：当x＞3时，x+b＞kx+6，
即不等式x+b＞kx+6的解集为x＞3．