题目内容
直线y=kx+b与抛物线y=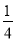
x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为_______________________．
（0，4）
【解析】【解析】
∵直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，∴kx+b=，
化简，得 x2﹣4kx﹣4b=0，∴x1+x2=4k，x1x2=﹣4b．
又∵OA⊥OB，∴ ，
解得，b=4，即直线y=kx+4，故直线恒过顶点（0，4）．
故答案为：（0，4）．
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案如图，将?ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（ ）
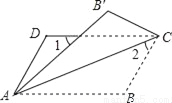
A. 66° B. 104° C. 114° D. 124°
C
【解析】试题解析：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ACD=∠BAC，
由折叠的性质得：∠BAC=∠B′AC，
∴∠BAC=∠ACD=∠B′AC=
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°；
故选C． 如图，四边形ABCD是平行四边形，AE平分∠BAD，交DC的延长线于点E．求证：DA=DE．
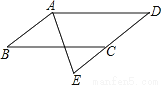
证明见解析.
【解析】试题分析：由平行四边形的性质得出AB∥CD，得出内错角相等∠E=∠BAE，再由角平分线证出∠E=∠DAE，即可得出结论．
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠E=∠BAE，∵AE平分∠BAD，∴∠BAE=∠DAE，∴∠E=∠DAE，∴DA=DE． 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（ ）
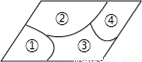
A. ①，② B. ①，④ C. ③，④ D. ②，③
D
【解析】分析：本题考查的是平行四边形的性质.
解析：破碎的玻璃中的②和③是连接的，可以得到四边形的大小.
故选B. 某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．
（1）求y与x之间的函数关系式；
（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？
（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？
（1）y=﹣30x+2100．（2）每件售价定为55元时，每星期的销售利润最大，最大利润6750元．
（3）每星期至少要销售该款童装360件．
【解析】试题分析：（1）根据售量y（件）与售价x（元/件）之间的函数关系即可得到结论．
（2））设每星期利润为W元，构建二次函数利用二次函数性质解决问题．
（3）列出不等式先求出售价的范围，再确定销售数量即可解决问题．
试题解... 抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A. 抛物线于x轴的一个交点坐标为（﹣2，0）
B. 抛物线与y轴的交点坐标为（0，6）
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
C
【解析】【解析】
当x=﹣2时，y=0，∴抛物线过（﹣2，0），∴抛物线与x轴的一个交点坐标为（﹣2，0），故A正确；
当x=0时，y=6，∴抛物线与y轴的交点坐标为（0，6），故B正确；
当x=0和x=1时，y=6，∴对称轴为x=，故C错误；
当x＜时，y随x的增大而增大，∴抛物线在对称轴左侧部分是上升的，故D正确；
故选C． 在下列y关于x的函数中，一定是二次函数的是（ ）
A. y=2x2 B. y=2x﹣2 C. y=ax2 D.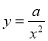 
A
【解析】解：A．是二次函数，故A符合题意；
B．是一次函数，故B错误；
C．a=0时，不是二次函数，故C错误；
D．a≠0时是分式方程，故D错误；
故选A． 世界杯决赛分成8个小组，每小组4个队，小组进行单循环（每个队都与该小组的其他队比赛一场）比赛，选出2个队进入16强，胜一场得3分，平一场得1分，负一场得0分．
（1）求每小组共比赛多少场？
（2）在小组比赛中，现有一队得到6分，该队出线是一个确定事件，还是不确定事件？
（1）6；（2）该队出线是一个不确定事件；
【解析】试题分析：（1）利用单循环的方法进行计算即可．
（2）根据必然事件、不可能事件、随机事件的概念可区别各类事件．
试题解析：（1）4×3÷2 =6（场）
答：每小组共比赛6场。
（2）因为总共有6场比赛，每场比赛最多可得3分，则6场比赛最多共有3×6=18分，现有一队得6分，还剩下12分，则还有可能有2个队同时得6分，... 如图,如果将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中四边形ACED的面积为_____.
15
【解析】试题分析：：设点A到BC的距离为h，根据平移的性质用BC表示出AD、CE，然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解．
试题解析：设点A到BC的距离为h，则S△ABC=BC•h=5，
∵平移的距离是BC的长的2倍，
∴AD=2BC，CE=BC，
∴四边形ACED的面积=（AD+CE）•h=（2BC+BC）•h=3×BC•h=3×5=15...