��Ŀ����
1��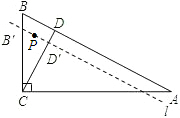 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=$6\sqrt{3}$cm��BC=6cm������A��B��ֱ��l��1cm/����ٶ�����������ƽ���˶�����BC�ڵ�B�䣬��CD�ڵ� D�䣬���ͬʱ����P�ӵ�B���������ֱ��l����1cm/����ٶ���ֱ��l�����·����������˶����������˶���ʱ��Ϊt�룮
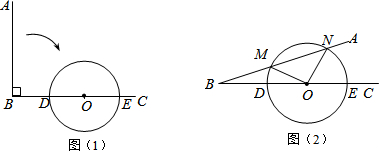
��ͼ����Rt��ABC�У���ACB=90�㣬AC=$6\sqrt{3}$cm��BC=6cm������A��B��ֱ��l��1cm/����ٶ�����������ƽ���˶�����BC�ڵ�B�䣬��CD�ڵ� D�䣬���ͬʱ����P�ӵ�B���������ֱ��l����1cm/����ٶ���ֱ��l�����·����������˶����������˶���ʱ��Ϊt�룮��1���������AB�ij���12cm��
��2������C��CD��AB�ڵ�D��tΪ��ֵʱ����P�ƶ���CD�ϣ�
��3��tΪ��ֵʱ���Ե�PΪԲ�ġ�1cmΪ�뾶��Բ��ֱ��CD���У�
��4���Ե�PΪԲ�ġ�1cmΪ�뾶�ġ�P��CD���ڵ�ֱ���ཻʱ���Ƿ���ڵ�P���������㹹�ɵ��������ǵȱ������Σ������ڣ�ֱ��д��t��ֵ���������ڣ�˵�����ɣ�
���� ��1�����ݹ��ɶ���������ý����
��2������ɵá�BCD=30�㣬���ݺ�30���ֱ�������ε����ʼ�����ý����
��3������ɷ�������������ٵ���P��CD��࣬��P��CD��һ������ʱ���ڵ���P��CD�Ҳ࣬��P��CD�ڶ�������ʱ������ֱ�ߺ�Բ��λ�ù�ϵ���з�����
��4������ɷ�������������ٵ���P��CD��࣬�ڵ���P��CD�Ҳ࣬��ϵȱ������ε����ʷ�����
��� �⣺��1���ߡ�ACB=90�㣬AC=$6\sqrt{3}$cm��BC=6cm��
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}=12$cm��
�ʴ�Ϊ��12cm��
��2������Rt��ABC�У���ACB=90�㣬AC=$6\sqrt{3}$cm��BC=6cm��
�ɵá�BCD=30�㣬
�൱��P�ƶ���CD��ʱ����6-t=2t��
��ã�t=2��
��t=2ʱ����P�ƶ���CD�ϣ�
��3���ٵ���P��CD��һ������ʱ������ֱ�ߺ�Բ���У���Բ�ĵ�ֱ�ߵľ������Բ�İ뾶���ã�
3-$\frac{3}{2}$t=1����ã�t=$\frac{4}{3}$��
�ڡ�P��CD�ڶ�������ʱ������ֱ�ߺ�Բ���У���Բ�ĵ�ֱ�ߵľ������Բ�İ뾶���ã�
$\frac{3}{2}$t-3=1����ã�t=$\frac{8}{3}$��
��t=$\frac{4}{3}$��t=$\frac{8}{3}$��
��4���ٵ���P��CD��࣬��P���������㹹�ɵ��������ǵȱ������Σ�2-t=$\frac{\sqrt{3}}{2}$��
��ã�t=2-$\frac{\sqrt{3}}{2}$��
�ڵ���P��CD�Ҳ࣬��P���������㹹�ɵ��������ǵȱ������Σ�t-2=$\frac{\sqrt{3}}{2}$��
��ã�t=2+$\frac{\sqrt{3}}{2}$��
���� ���⿼����һ�κ����ۺ��⣮����ʱ��Ҫ��ѧ�����н�ֱ�������Ρ�ֱ�ߺ�Բ��λ�ù�ϵ��֪ʶ���ۺ�Ӧ���������ѶȽϴ��⿼��Բ���ۺ����⣬֪ʶ��࣬�ؼ��Ǹ���Բ��ֱ�ߵĹ�ϵ���з�����

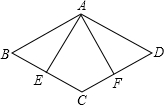 ������ABCD�У�AE��BC�ڵ�E��AF��CD�ڵ�F����E��F�ֱ�ΪBC��CD���е㣬���EAF���ڣ�������
������ABCD�У�AE��BC�ڵ�E��AF��CD�ڵ�F����E��F�ֱ�ΪBC��CD���е㣬���EAF���ڣ�������| A�� | 60�� | B�� | 55�� | C�� | 45�� | D�� | 30�� |
| A�� | ��-a����-a��2=-a3 | B�� | -2x2��-3x��=-6x4 | C�� | ��-a��3��-a��2=-a5 | D�� | ��-a��3��-a��3=a6 |

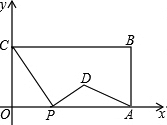 ��ͼ����ƽ��ֱ������ϵ�У�����OABC������OA��OC�ֱ���x�ᡢy����������ϣ�OA=6��OC=4����P�ӵ�O��������x����ÿ��1����λ�����ٶ����A�����˶�������P�����Aʱֹͣ�˶������P�˶���ʱ����t�룮���߶�CP���е��Ƶ�P��˳ʱ�뷽����ת90��õ�D����D���P���˶����˶�������DP��DA����
��ͼ����ƽ��ֱ������ϵ�У�����OABC������OA��OC�ֱ���x�ᡢy����������ϣ�OA=6��OC=4����P�ӵ�O��������x����ÿ��1����λ�����ٶ����A�����˶�������P�����Aʱֹͣ�˶������P�˶���ʱ����t�룮���߶�CP���е��Ƶ�P��˳ʱ�뷽����ת90��õ�D����D���P���˶����˶�������DP��DA����