题目内容
15.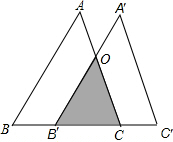 如图,将边长为3$\sqrt{2}$的等边△ABC沿BC方向向右平移得到△A′B′C′,若△ABC与△A′B′C重叠部分面积为2$\sqrt{3}$,则此次平移的距离是( )
如图,将边长为3$\sqrt{2}$的等边△ABC沿BC方向向右平移得到△A′B′C′,若△ABC与△A′B′C重叠部分面积为2$\sqrt{3}$,则此次平移的距离是( )| A. | 3$\sqrt{2}$-2 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 重叠部分为等边三角形,设B1C=x,则B1C边上的高为$\frac{\sqrt{3}}{2}x$,根据重叠部分的面积列方程求x,再求BB1.
解答 解:设B1C=x,
根据等边三角形的性质可知,重叠部分为等边三角形,
则B1C边上的高为$\frac{\sqrt{3}}{2}$x,
∴$\frac{1}{2}$×x×$\frac{\sqrt{3}}{2}$x=2$\sqrt{3}$,解得x=2$\sqrt{2}$(舍去负值),
∴B1C=2$\sqrt{2}$,
∴BB1=BC-B1C=3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$.
故选B
点评 本题考查了等边三角形的性质,平移的性质.关键是判断重叠部分图形为等边三角形,利用等边三角形的性质求边长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.连掷两枚质地均匀的骰子,它们的点数相同的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
4.如果把分式$\frac{2n}{m-n}$中的m和n都扩大2倍,那么分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 缩小2倍 | D. | 扩大4倍 |
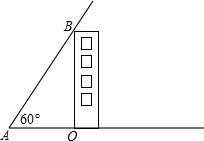 请从以下两个小题中个任意选一作答,若对选,则按第一题计分.
请从以下两个小题中个任意选一作答,若对选,则按第一题计分.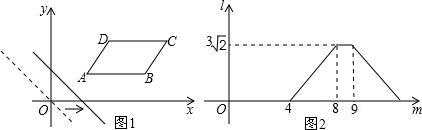
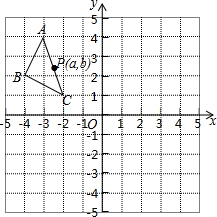 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.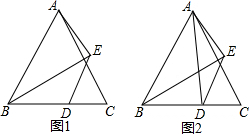 如图,△ABC为等边三角形,点E在∠ABC的平分线上,点D在BC边上,连接AE、DE,且∠AED=120°.
如图,△ABC为等边三角形,点E在∠ABC的平分线上,点D在BC边上,连接AE、DE,且∠AED=120°.