题目内容
5.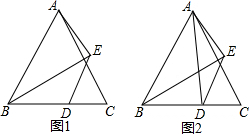 如图,△ABC为等边三角形,点E在∠ABC的平分线上,点D在BC边上,连接AE、DE,且∠AED=120°.
如图,△ABC为等边三角形,点E在∠ABC的平分线上,点D在BC边上,连接AE、DE,且∠AED=120°.(1)求证:AB+BD=$\sqrt{3}$BE;
(2)连接AD,若BE=$\frac{13\sqrt{3}}{3}$,AD=7,求线段BD的长.
分析 (1)过E作EM⊥AB于M,EN⊥BC于N,证△AME≌△DNE,根据全等得出AM=CN,证△BEM≌△BEN,根据全等三角形的性质得出BM=BN,即可求出AB+BD=2BM,即可得出答案;
(2)求出AB+BD=13,设BD=x,则AB=13-x,过D作DF⊥AB于F,解直角三角形求出BF=$\frac{1}{2}$BD=$\frac{x}{2}$,DF=$\sqrt{3}$BD=$\frac{\sqrt{3}x}{2}$,AF=$\frac{26-3x}{2}$,根据勾股定理得出方程72=($\frac{\sqrt{3}x}{2}$)2+($\frac{26-3x}{2}$)2,求出方程的解即可.
解答 (1)证明:如图1,过E作EM⊥AB于M,EN⊥BC于N,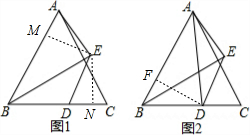 则∠BME=∠BNE=∠AME=90°,
则∠BME=∠BNE=∠AME=90°,
∵BE平分∠ABC,
∴∠MBE=∠NBE,EM=EN,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠MEN=360°-90°-90°-60°=120°,
∵∠AED=120°,
∴∠AED=∠MEN=120°,
∴∠AEM=∠DEN=120°-∠MED,
在△AME和△DNE中,
$\left\{\begin{array}{l}{∠AME=∠DNE}\\{ME=NE}\\{∠AEM=∠DEN}\end{array}\right.$,
∴△AME≌△DNE(ASA),
∴AM=DN,
在△BEM和△BEN中,
$\left\{\begin{array}{l}{∠BME=∠BNE}\\{∠MBE=∠NBE}\\{BE=BE}\end{array}\right.$,
∴△BEM≌△BEN(AAS),
∴BM=BN,
∴AB+BD
=BM+AM+BN-DN
=2BM,
∵∠ABC=60°,BE平分∠ABC,
∴∠ABE=30°,
∴BM=$\frac{\sqrt{3}}{2}$BE,
即AB+BD=2×$\frac{\sqrt{3}}{2}$BE=$\sqrt{3}$BE;
(2)解:∵AB+BD=$\sqrt{3}$BE=$\sqrt{3}$×$\frac{13\sqrt{3}}{3}$=13,
∴设BD=x,则AB=13-x,
如图2,过D作DF⊥AB于F,
则∠DFB=90°,
∵∠ABC=60°,
∴∠FDB=30°,
∴BF=$\frac{1}{2}$BD=$\frac{x}{2}$,DF=$\sqrt{3}$BD=$\frac{\sqrt{3}x}{2}$,
则AF=13-x-$\frac{x}{2}$=$\frac{26-3x}{2}$,
在Rt△AFD中,由勾股定理得:AD2=DF2+AF2,
72=($\frac{\sqrt{3}x}{2}$)2+($\frac{26-3x}{2}$)2,
解得:x=5或8,
当x=8时,BD=8,AB=13-8=5<7,此时不符合题意舍去,
即BD的长是5.
点评 本题考查了全等三角形的性质和判定,勾股定理,解直角三角形的应用,能综合运用知识点进行计算和推理是解此题的关键,题目比较好,难度偏大.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案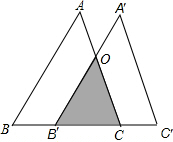 如图,将边长为3$\sqrt{2}$的等边△ABC沿BC方向向右平移得到△A′B′C′,若△ABC与△A′B′C重叠部分面积为2$\sqrt{3}$,则此次平移的距离是( )
如图,将边长为3$\sqrt{2}$的等边△ABC沿BC方向向右平移得到△A′B′C′,若△ABC与△A′B′C重叠部分面积为2$\sqrt{3}$,则此次平移的距离是( )| A. | 3$\sqrt{2}$-2 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
| 成绩(环) | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | 2 | 7 | 6 | 3 | 1 |
| A. | 1.7×104 | B. | 1.7×108 | C. | 1.7×1012 | D. | 1.7×1013 |
 如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )
如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )| A. | 20° | B. | 40° | C. | 50° | D. | 60° |
