题目内容
2. 如图,在△ABC中,∠B=90°,∠A=60°,AB=1,作等腰三角形△ACD,使∠CAD=30°,且点D和B位于AC异侧,连结BD交AC于点O
如图,在△ABC中,∠B=90°,∠A=60°,AB=1,作等腰三角形△ACD,使∠CAD=30°,且点D和B位于AC异侧,连结BD交AC于点O(1)请在所给图形基础上画出符合要求的其中一个草图,并在图中找出相似三角形后说明理由
(2)在(1)的条件下,求出AO长.
分析 (1)根据△ACD是等腰三角形,∠CAD=30°,且点D和B位于AC异侧,进行作图;根据AD∥BC,即可得出△AOD∽△COB;
(2)分三种情况进行讨论:①AD=CD;②AD=AC;③AC=DC,分别根据等腰三角形的性质,以及相似三角形的性质进行计算求解.
解答  解:(1)如图所示,等腰三角形△ACD即为所求;
解:(1)如图所示,等腰三角形△ACD即为所求;
图中,△AOD∽△COB,
理由:∵△ABC中,∠ABC=90°,∠BAC=60°,而∠CAD=30°,
∴∠ABC+∠BAD=180°,
∴AD∥BC,
∴△AOD∽COB;
(2)①如图所示,当AD=CD时,过D作DE⊥AC于E,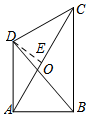
∵AD=CD,∠CAD=30°,
∴AE=$\frac{1}{2}$AC,AD=2DE,
∵△ABC中,∠ABC=90°,∠BAC=60°,AB=1,
∴AC=2AB=2,BC=$\sqrt{3}$,
∴AE=1,
∴Rt△AED中,DE=$\frac{\sqrt{3}}{3}$,AD=2DE=$\frac{2}{3}\sqrt{3}$,
∵△AOD∽COB,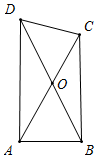
∴$\frac{AO}{CO}$=$\frac{AD}{CB}$,即$\frac{AO}{2-AO}$=$\frac{\frac{2}{3}\sqrt{3}}{\sqrt{3}}$,
解得AO=$\frac{4}{5}$;
②如图所示,当AD=AC=2时,
根据△AOD∽△COB可得,$\frac{AO}{CO}$=$\frac{AD}{CB}$,
即$\frac{AO}{2-AO}$=$\frac{2}{\sqrt{3}}$,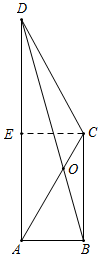
解得AO=8-4$\sqrt{3}$;
③如图所示,当AC=CD时,过C作CE⊥AD,则
四边形ABCE是矩形,即AE=BC=$\sqrt{3}$,
∵AC=CD,
∴AD=2AE=2$\sqrt{3}$,
根据△AOD∽△COB可得,$\frac{AO}{CO}$=$\frac{AD}{CB}$,
即$\frac{AO}{2-AO}$=$\frac{2\sqrt{3}}{\sqrt{3}}$,
解得AO=$\frac{4}{3}$.
综上所述,AO长为$\frac{4}{5}$或8-4$\sqrt{3}$或$\frac{4}{3}$.
点评 本题主要考查了等腰三角形的性质以及相似三角形的判定与性质的综合应用,解决问题的关键是根据题意画出图形,解题时注意分类思想的运用.

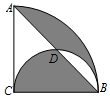 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )| A. | π-1 | B. | 2π-1 | C. | 2π-2 | D. | π-2 |
| A. | 底边对应相等的两个等腰三角形全等 | |
| B. | 腰对应相等的两个等腰三角形全等 | |
| C. | 斜边对应相等的两个直角三角形全等 | |
| D. | 面积相等的两个等边三角形全等 |