题目内容
16. 如图,抛物线y=-x2+20的图象与y轴正半轴的交点为A,将线段OA分成20等份,设分点分别为P1,P2,…,P19,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,记△OP1Q1,△P1P2Q2,…的面积分别为S1,S2,…,S19,则S12+S22+…+S192的值为( )
如图,抛物线y=-x2+20的图象与y轴正半轴的交点为A,将线段OA分成20等份,设分点分别为P1,P2,…,P19,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,记△OP1Q1,△P1P2Q2,…的面积分别为S1,S2,…,S19,则S12+S22+…+S192的值为( )| A. | 47 | B. | 47.5 | C. | 48 | D. | 48.5 |
分析 根据等分求出OP1=P1P2=P2P3=P3P4=…=P18P19=1,再利用抛物线解析式求出P1Q1,P2Q2,…,P19Q19的平方的值,利用三角形的面积表示出S1,S2,…,并平方后相加,然后根据等差数列求和公式进行计算即可得解.
解答 解:∵P1,P2,…,P19将线段OA分成20等份,
∴OP1=P1P2=P2P3=P3P4=…=P18P19=1,
∵过分点P1作y轴的垂线,与抛物线交于点Q1,
∴-x2+20=1,
解得x2=19,
∴S12=($\frac{1}{2}$×1×P1Q1)2=$\frac{1}{4}$×19,
同理可得S22=$\frac{1}{4}$×18,
S32=$\frac{1}{4}$×17,
…
S192=$\frac{1}{4}$×1,
∴w=S12+S22+S32+…+S192
=$\frac{1}{4}$×19+$\frac{1}{4}$×18+$\frac{1}{4}$×17+…+$\frac{1}{4}$×1
=$\frac{1}{4}$×$\frac{19×(19+1)}{2}$
=47.5,
故选B.
点评 本题是对二次函数的综合考查,根据图形的变化规律,分别表示出各三角形的面积的平方是解题的关键.

练习册系列答案
相关题目
6. 如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )
如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )
 如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )
如图是一次函数y=kx+b的图象,当y<-2时,x的取值范围是( )| A. | x<3 | B. | x>3 | C. | x<-1 | D. | x>-1 |
8.计算|-$\frac{3}{2}$|+1的结果是( )
| A. | $\frac{5}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |

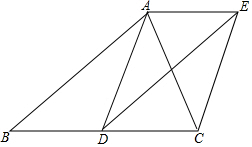 如图所示,已知AD是△ABC的中线,DE∥AB,且DE=AB,连结AE,EC,求证:四边形ADCE是平行四边形.
如图所示,已知AD是△ABC的中线,DE∥AB,且DE=AB,连结AE,EC,求证:四边形ADCE是平行四边形. (1)如图,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{7}{22}$∠AOE,求∠EOG和∠DOF的度数.
(1)如图,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{7}{22}$∠AOE,求∠EOG和∠DOF的度数. 如图,在Rt△ABC中,∠C=90°,AC>BC,请用尺规作图方法把它分成两个三角形,且其中至少有一个是等腰三角形(保留作图痕迹,不写作法)
如图,在Rt△ABC中,∠C=90°,AC>BC,请用尺规作图方法把它分成两个三角形,且其中至少有一个是等腰三角形(保留作图痕迹,不写作法)