题目内容
3.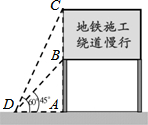 某市备受关注的地铁六号线正紧张施工,为了缓解一些施工路段交通拥挤的现状,交警队设立了如图所示的交通略况显示牌,已知立杆AB的高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况显示牌BC的高度.
某市备受关注的地铁六号线正紧张施工,为了缓解一些施工路段交通拥挤的现状,交警队设立了如图所示的交通略况显示牌,已知立杆AB的高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况显示牌BC的高度.
分析 在Rt△ABD中,知道了已知角的对边,可用正切函数求出邻边AD的长;同理在Rt△ABC中,知道了已知角的邻边,用正切值即可求出对边AC的长,进而由BC=AC-AB得解.
解答 解:∵在Rt△ADB中,∠BDA=45°,∠BAD=90°,AB=3m,
∴AD=3m.
在Rt△ADC中,∠CDA=60°,
∴tan60°=$\frac{CA}{AD}$,
∴AC=3$\sqrt{3}$.
∴BC=AC-AB=(3$\sqrt{3}$-3)m.
答:路况显示牌BC的高度是(3$\sqrt{3}$-3)m.
点评 此题主要考查了解直角三角形的应用,当两个直角三角形有公共边时,先求出这条公共边的长是解答此类题的一般思路.

练习册系列答案
相关题目
14.下列命题中,真命题是( )
| A. | 底边对应相等的两个等腰三角形全等 | |
| B. | 腰对应相等的两个等腰三角形全等 | |
| C. | 斜边对应相等的两个直角三角形全等 | |
| D. | 面积相等的两个等边三角形全等 |
8.计算|-$\frac{3}{2}$|+1的结果是( )
| A. | $\frac{5}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
15.某区今年暑假选派了180名教师担任G20交通引导志愿者、80名教师担任安全维护志愿者,现要把一部分安全维护志愿者调到交通引导志愿者队伍中,使安全维护志愿者人数占交通引导志愿者人数的30%,设把x名安全维护志愿者调到交通引导志愿者队伍中,则可列方程( )
| A. | 80-x=30%×(180+x) | B. | 80-x=30%×180 | C. | 180+x=30%×(80-x) | D. | 80-x=30%×260 |
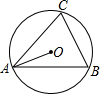 如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的大小为70度.
如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的大小为70度.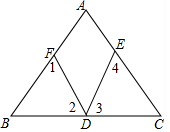 如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.
如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.