题目内容
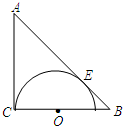 已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.
已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求:⊙O的半径.
考点:切线的性质
专题:计算题
分析:连接OE,如图,根据等腰直角三角形的性质得AB=
AC=
,∠B=45°,利用AC⊥BC可判断AC为⊙O的切线,而AE是⊙O的切线,根据切线长定理得AC=AE=1,根据切线的性质得OE⊥AB,然后证明△OBE为等腰直角三角形,所以OE=BE=AB-AE=
-1.
| 2 |
| 2 |
| 2 |
解答:解:连接OE,如图,
∵△ABC是等腰直角三角形,
∴AB=
AC=
,∠B=45°,
∵AC⊥BC,
∴AC为⊙O的切线,
∵AE是⊙O的切线,
∴AC=AE=1,且OE⊥AB,
在Rt△OBE中,∵∠B=45°,
∴△OBE为等腰直角三角形,
∴OE=BE=AB-AE=
-1,
即⊙O半径长为
-1.

∵△ABC是等腰直角三角形,
∴AB=
| 2 |
| 2 |
∵AC⊥BC,
∴AC为⊙O的切线,
∵AE是⊙O的切线,
∴AC=AE=1,且OE⊥AB,
在Rt△OBE中,∵∠B=45°,
∴△OBE为等腰直角三角形,
∴OE=BE=AB-AE=
| 2 |
即⊙O半径长为
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.也考查了等腰直角三角形的性质.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
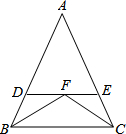 如图△ABC中,∠B、∠C的角平分线交于点F,过F作DE∥BC交AB于D,交AC于E,下列结论:①△BDF,△ADE都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB+AC;④BF=CF;⑤若∠A=80°,则∠BFC=130°,其中正确的有( )
如图△ABC中,∠B、∠C的角平分线交于点F,过F作DE∥BC交AB于D,交AC于E,下列结论:①△BDF,△ADE都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB+AC;④BF=CF;⑤若∠A=80°,则∠BFC=130°,其中正确的有( )| A、2个 | B、3个 | C、4个 | D、5个 |
一组数据:2,4,5,6,x的平均数是4,则这组数的标准差是( )
| A、2 | ||
B、
| ||
| C、10 | ||
D、
|
下列图形中,∠1与∠2互为对顶角的是( )
A、 |
B、 |
C、 |
D、 |
下列运算正确的是( )
| A、a2a3=a6 |
| B、2x2-x2=1 |
| C、8x4÷(-4x)=-2x3 |
| D、a3=3a |
 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.