题目内容
 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.考点:旋转的性质
专题:计算题
分析:如图,作B′E⊥AC交CA的延长线于E,利用含30度的直角三角形三边的关系得AC=
AB=1,再根据旋转的性质得AB=AB′=2,∠B′AB=60°,则∠EAB′=180°-∠B′AB-∠BAC=60°,可计算出∠AB′E=30°,所以AE=1,在Rt△AB′E中利用勾股定理可计算出B′E=
,则EC=AE+AC=2,然后在Rt△CEB′中根据勾股定理可计算出B′C=
.
| 1 |
| 2 |
| 3 |
| 7 |
解答:解:如图,作B′E⊥AC交CA的延长线于E,
∵∠ACB=90°,∠BAC=60°,AB=2,
∴∠ABC=30°,
∴AC=
AB=1,
∵Rt△AB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,
∴AB=AB′=2,∠B′AB=60°,
∴∠EAB′=180°-∠B′AB-∠BAC=60°,
∵B′E⊥EC,
∴∠AB′E=30°,
∴AE=1,
在Rt△AB′E中,∵AE=1,AB′=2,
∴B′E=
=
,
∴EC=AE+AC=2,
在Rt△CEB′中,∵B′E=
,CE=2,
∴B′C=
=
.

∵∠ACB=90°,∠BAC=60°,AB=2,
∴∠ABC=30°,
∴AC=
| 1 |
| 2 |
∵Rt△AB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,
∴AB=AB′=2,∠B′AB=60°,
∴∠EAB′=180°-∠B′AB-∠BAC=60°,
∵B′E⊥EC,
∴∠AB′E=30°,
∴AE=1,
在Rt△AB′E中,∵AE=1,AB′=2,
∴B′E=
| AB′2-AE2 |
| 3 |
∴EC=AE+AC=2,
在Rt△CEB′中,∵B′E=
| 3 |
∴B′C=
| B′E2+CE2 |
| 7 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理.

练习册系列答案
相关题目
 如图,把一根绳子先剪成一样长的两段后重叠在一起如线段AB,再从P处将其剪断,已知AP=
如图,把一根绳子先剪成一样长的两段后重叠在一起如线段AB,再从P处将其剪断,已知AP= 如图,平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?说说你的理由.
如图,平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?说说你的理由. 如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.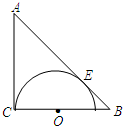 已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.
已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.