题目内容
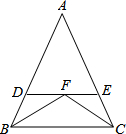 如图△ABC中,∠B、∠C的角平分线交于点F,过F作DE∥BC交AB于D,交AC于E,下列结论:①△BDF,△ADE都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB+AC;④BF=CF;⑤若∠A=80°,则∠BFC=130°,其中正确的有( )
如图△ABC中,∠B、∠C的角平分线交于点F,过F作DE∥BC交AB于D,交AC于E,下列结论:①△BDF,△ADE都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB+AC;④BF=CF;⑤若∠A=80°,则∠BFC=130°,其中正确的有( )| A、2个 | B、3个 | C、4个 | D、5个 |
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:证明DB=DF,EF=EC;进而判断②③正确;当∠A=80°时,求出∠BFC=130°,得到⑤正确,即可解决问题.
解答: 解:如图,∵∠B、∠C的角平分线交于点F,
解:如图,∵∠B、∠C的角平分线交于点F,
∴∠DBF=∠CBF(设为α),∠ECF=∠BCF(设为β);
∵DE∥BC,
∴∠DFB=∠CBF=α,∠EFC=∠BCF=β;
∴∠DBF=∠DFB,∠EFC=∠ECF,
∴DB=DF,EF=EC;
∴②③正确;
∵∠A=80°,
∴∠FBC+∠FCB=
=50°,
∴∠BFC=180°-50°=130°,
故⑤正确;
故选B.
 解:如图,∵∠B、∠C的角平分线交于点F,
解:如图,∵∠B、∠C的角平分线交于点F,∴∠DBF=∠CBF(设为α),∠ECF=∠BCF(设为β);
∵DE∥BC,
∴∠DFB=∠CBF=α,∠EFC=∠BCF=β;
∴∠DBF=∠DFB,∠EFC=∠ECF,
∴DB=DF,EF=EC;
∴②③正确;
∵∠A=80°,
∴∠FBC+∠FCB=
| 180°-80° |
| 2 |
∴∠BFC=180°-50°=130°,
故⑤正确;
故选B.
点评:该题主要考查了等腰三角形的判定、平行线的性质等几何知识点的应用问题;灵活运用等腰三角形的判定、平行线的性质是解题的关键.

练习册系列答案
相关题目
设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只.则从中任意取1只,是二等品的概率等于( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
 如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上. 在直角三角形ABC中,∠ACB=90°,CE为高,AF为角平分线,
在直角三角形ABC中,∠ACB=90°,CE为高,AF为角平分线,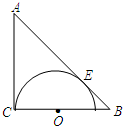 已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.
已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.