题目内容
13.已知|a-1|+|ab+3|=0,求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+98)(b+98)}$.分析 根据非负数的性质列出算式,求出a、b的值,计算即可.
解答 解:由题意得,a-1=0,ab+3=0,
解得,a=1,b=3,
则$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+98)(b+98)}$
=$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{99×101}$
=2×(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{99}$-$\frac{1}{101}$)
=2×$\frac{301}{202}$
=$\frac{301}{101}$.
点评 本题考查的是非负数的性质,掌握当几个非负数或式的绝对值相加和为0时,则其中的每一项都必须等于0是解题的关键.

练习册系列答案
相关题目
7. 数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
 数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )
数a、b、c在数轴上对应的位置如图,化简|a+b|-|c-b|的结果( )| A. | a+c | B. | c-a | C. | -c-a | D. | a+2b-c |
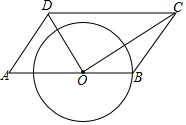 如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由.
如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由. 已知,如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.
已知,如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.
 一个运动员推铅球,铅球在点A处出手,出手时铅球离地面$\frac{7}{6}$m,铅球运行时距离地面的最大高度CD是2.5m,此时铅球验水平方向行进了4m,铅球落地点在斜坡上的点B处,已知铅球经过的路线是抛物线,现以铅球出手点A所在的铅垂线OA的方向为y轴正方向,以铅垂线与地面的交点为点O建立直角坐标系,斜坡可以用一次函数y=$\frac{1}{4}$x刻画.
一个运动员推铅球,铅球在点A处出手,出手时铅球离地面$\frac{7}{6}$m,铅球运行时距离地面的最大高度CD是2.5m,此时铅球验水平方向行进了4m,铅球落地点在斜坡上的点B处,已知铅球经过的路线是抛物线,现以铅球出手点A所在的铅垂线OA的方向为y轴正方向,以铅垂线与地面的交点为点O建立直角坐标系,斜坡可以用一次函数y=$\frac{1}{4}$x刻画.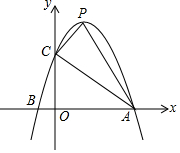 已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.
已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.