题目内容
2.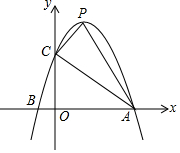 已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.
已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.(1)求四边形OAPC的面积;
(2)判断△PCA的形状,并说明埋由;
(3)△COB与△PCA相似吗?如果相似,请证明:如果不相似,请说明理由.
分析 (1)直接用坐标轴上,点的特点和顶点坐标公式即可;再用坐标系中几何图形的面积计算方法直接计算即可;
(2)用勾股定理逆定理直接判断即可;
(3)用三边对应成比例,两三角形相似判断即可.
解答 解:(1)∵抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,
∴A(3,0),B(-1,0),C(0,3),顶点P(1,4),
∴直线AC的解析式为y=-x+3,
∴当x=1时,y=2,
∴S四边形OAPC=$\frac{1}{2}$×3×3+$\frac{1}{2}$(4-2)×1+$\frac{1}{2}$(4-2)×2=$\frac{15}{2}$;
(2)由(1)知,A(3,0),C(0,3),P(1,4),
∴AC2=18,AP2=4+16=20,CP2=2,
∴AP2=AC2+CP2,
∴△ACP是直角三角形,
(3)△COB∽△ACP.
证明:由(2)知,AC=3$\sqrt{2}$,AP=2$\sqrt{5}$,CP=$\sqrt{2}$,
由(1)知,B(-1,0),C(0,3),
∴OB=1,OC=3,BC=$\sqrt{10}$,
∴$\frac{CP}{OB}=\sqrt{2}$,$\frac{AC}{OC}=\frac{3\sqrt{2}}{3}$=$\sqrt{2}$,$\frac{AP}{BC}=\sqrt{2}$
∴$\frac{CP}{OB}=\frac{AC}{OC}=\frac{AP}{BC}$,
∴△COB∽△ACP.
点评 此题是二次函数综合题,主要考查了坐标轴上点的特点,和顶点坐标公式,几何图形面积的计算方法,勾股定理逆定理,相似三角形的判定,是一道比较简单的数形结合的题目.

练习册系列答案
相关题目
16.宜昌市西陵区计划到2017年实现总收入4600亿元,这个数据用科学记数法表示为( )亿元.
| A. | 4.6×103 | B. | 4.6×104 | C. | 46×102 | D. | 0.46×104 |
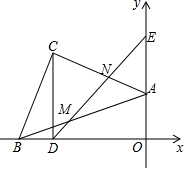 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在x轴的负半轴上,△ABC为等腰直角三角形,AC=BC,CD⊥x轴于点D,连接DE交AB于点M,若D(a,0)E(0,b),且满足b2+2ab+2b2-12b+36=0
如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在x轴的负半轴上,△ABC为等腰直角三角形,AC=BC,CD⊥x轴于点D,连接DE交AB于点M,若D(a,0)E(0,b),且满足b2+2ab+2b2-12b+36=0