��Ŀ����
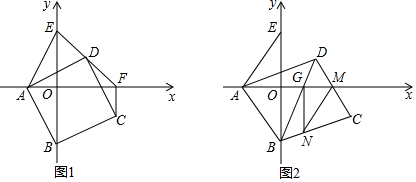
18����ͼ��ʾ����ֱ֪��y=-$\frac{1}{2}$x+4�ֱ���x�ᣬy�ύ�ڵ�A��B��CΪOB���е㣬��P���߶�OA�ϵĶ��㣬��PΪֱ�Ƕ��㣬PCΪ������PC���Ҳ�����ֱ��������PCD����OP=m����1��ֱ��д��OA=8��OB=4��
��2����mΪ��ֵʱ����D��ֱ��AB�ϣ�
��3������AD���ڵ�P���˶������У��Ƿ����mʹ�á�PAD���ڡ�PDA���PCO�������ڣ������m��ֵ���������ڣ���˵�����ɣ�
���� ��1���ȸ���ֱ�߽���ʽ�ó���A��B�����꣬���ɵó�OA��OB��
��2�����жϳ�AE=2DE��OC=2���ٸ���ͬ�ǵ������ȵó���EPD=��OCP�������жϳ���COP�ա�PED���ó�PE=2�����ɵó�OP=2�����ɵó����ۣ�
��3���ٵ���PAD=��PDAʱ�����ɵó�PD=PA�����ɵó�OP=8-PA������ù��ɶ������ɵó�DE=2�����ɵó����ۣ�
�ڵ���PAD=��PCOʱ���ó���PAD=��APD�����ɵó�AD=PD��ͬ��2���ķ����жϳ���COP�ա�PED�����ɵó�PE=2�������ó�AP=4�����ɵó����ۣ�
��� �⣺��1����ֱ��y=-$\frac{1}{2}$x+4�ֱ���x�ᣬy�ύ�ڵ�A��B��
��A��8��0����B��0��4����
��OA=8��OB=4��
�ʴ�Ϊ��8��4��
��2����ͼ1�� ����D��DE��OA��
����D��DE��OA��
�ߵ�D��ֱ��AB�ϣ�
��tan��BAO=$\frac{DE}{AE}=\frac{OB}{OA}$=$\frac{4}{8}$=$\frac{1}{2}$��
��AE=2DE��
��CΪOB���е㣬
��OC=$\frac{1}{2}$OB=2��
�ߡ�CPD=90�㣬
���CPO+��EPD=90�㣬
�ߡ�CPO+��OCP=90�㣬
���EPD=��OCP��
�ڡ�COP�͡�PED�У�$\left\{\begin{array}{l}{��COP=��PED}\\{��OCP=��EPD}\\{PC=PD}\end{array}\right.$��
���COP�ա�PED��
��PE=OC=2��DE=OP��
��OP+PE+AE=8��
��DE+2+2DE=8��
��DE=2��
��OP=2��
��m=OP=2��
��3����ͼ2�� �ɣ�2��֪����OCP=��APD��
�ɣ�2��֪����OCP=��APD��
�ٵ���PAD=��PDAʱ��
��PD=PA��
��PC=PA��
��OA=8��
��OP=OA-PA=8-PA��
��Rt��OCP��OC=2��
���ݹ��ɶ����ã�PC2-OP2=OC2��
��PA2-��8-PA��2=4��
��PA=$\frac{17}{4}$��
��m=OP=8-$\frac{17}{4}$=$\frac{15}{4}$��
�ڵ���PAD=��PCOʱ��
���PAD=��APD��
��AD=PD��
����D��DE��AP��
��PA=PE=$\frac{1}{2}$AP��
�ߡ�CPD=90�㣬
���CPO+��EPD=90�㣬
�ߡ�CPO+��OCP=90�㣬
���EPD=��OCP��
�ڡ�COP�͡�PED�У�$\left\{\begin{array}{l}{��COP=��PED}\\{��OCP=��EPD}\\{PC=PD}\end{array}\right.$��
���COP�ա�PED��
��PE=OC=2��
��AP=2PE=4��
��OP+AP=8��
��OP=8-AP=4��
��m=OP=4��
���� ������һ�κ����ۺ��⣬��Ҫ������ֱ����������Ĺ�ϵ�����������ε����ʣ�ȫ�������ε��ж������ɶ������Ȿ��Ĺؼ����жϡ�COP�ա�PED����һ���е��Ѷȵ��п������⣮

 ��ͼ����ƽ��ֱ������ϵ�У���AOBΪ����ֱ��������A��4��4������C��O��������2����λ/����ٶ���x���������˶���
��ͼ����ƽ��ֱ������ϵ�У���AOBΪ����ֱ��������A��4��4������C��O��������2����λ/����ٶ���x���������˶���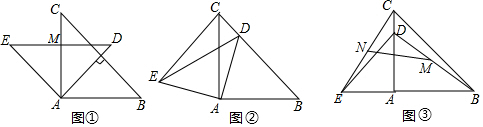
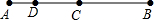 ��ͼ��C���߶�AB���е㣬D���߶�AC�ϣ�AD��DC=1��2����ͼ�������߶�֮��Ϊ26�����߶�AB�ij���7.8��
��ͼ��C���߶�AB���е㣬D���߶�AC�ϣ�AD��DC=1��2����ͼ�������߶�֮��Ϊ26�����߶�AB�ij���7.8��