题目内容
11.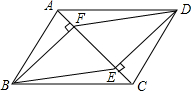 如图,在?ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E、F.
如图,在?ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E、F.(1)求证:四边形BEDF是平行四边形.
(2)若AB=13,AD=20,DE=12,求?BEDF的面积.
分析 (1)由平行四边形的性质得出AB=CD,AB∥CD,证出∠BAC=∠DCA,由垂线的性质得出BF∥DE,∠AFB=∠CED=90°,由AAS证明△ABF≌△CDE,得出BF=DE,AF=EC,即可得出四边形BEDF是平行四边形.
(2)由勾股定理求出EC,得出AF,由勾股定理求出AE,得出EF,即可得出?BEDF的面积.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
∵DE⊥AC,BF⊥AC,
∴BF∥DE,∠AFB=∠CED=90°,
在△ABF和△CDE中,
$\left\{\begin{array}{l}{∠BAC=∠DCA}&{\;}\\{∠AFB=∠CED}&{\;}\\{AB=CD}&{\;}\end{array}\right.$,
∴△ABF≌△CDE(AAS),
∴BF=DE,AF=EC,
∴四边形BEDF是平行四边形.
(2)∵AB=13,
∴CD=13,
∴EC=$\sqrt{C{D}^{2}-D{E}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴AF=5,
∵AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
∴EF=AE-AF=11,
∴?BEDF的面积=2×$\frac{1}{2}$×11×12=132.
点评 本题考查了平行四边形的判定与性质,全等三角形的判定与性质、勾股定理、垂线的性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如果不等式(1+a)x>1+a的解集为x<1,那么a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-1 | D. | a<-1 |
3.在以下实数$\frac{π}{3}$,$\frac{\sqrt{2}}{2}$,1.414,1.010010001…,42,$\frac{1}{6}$,0、$\root{3}{8}$、3π、$\frac{22}{7}$、$\frac{131}{11}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.周星驰的新春大片《美人鱼》创造了无数票房记录,从开始上映到3月6日9时止,票房累计达33亿元,33亿元用科学记数法表示为( )
| A. | 33×108元 | B. | 3.3×109元 | C. | 3.3×1010元 | D. | 0.33×1010元 |
 如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,抛物线y=ax2+bx+c经过O、A、E三点.
如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,抛物线y=ax2+bx+c经过O、A、E三点. 如图,是某射击运动员在一次射击训练时10次射击后的成绩(环数)制成的条形统计图,求这10次射击后的成绩的平均数、众数和中位数.
如图,是某射击运动员在一次射击训练时10次射击后的成绩(环数)制成的条形统计图,求这10次射击后的成绩的平均数、众数和中位数.