题目内容
6.解不等式组:$\left\{\begin{array}{l}{3x-1<2(x+1)}\\{\frac{x+3}{2}≥1}\end{array}\right.$.分析 分别解出两个不等式的解集,然后求出两个解集的公共部分即可.
解答 解:解不等式3x-1<2(x+1)得,x<3,
解不等式$\frac{x+3}{2}≥1$得,x≥-1,
即不等式组的解集为-1≤x<3.
点评 本题考查了解一元一次不等式组:求解出两个不等式的解集,然后按照“同大取大,同小取小,大于小的小于大的取中间,小于小的大于大的无解”确定不等式组的解集.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.(-$\frac{1}{2}$)2的平方根是( )
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |

 B.
B.  C.
C.  D.
D. 
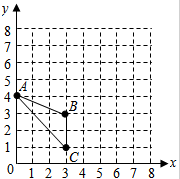 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.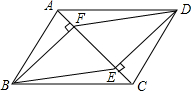 如图,在?ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E、F.
如图,在?ABCD中,DE⊥AC,BF⊥AC,垂足分别为点E、F.
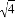 的值为( ).
的值为( ).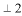 D. 4
D. 4