能使等式$\sqrt{\frac{x}{x-3}}$=$\frac{\sqrt{x}}{\sqrt{x-3}}$成立的条件是( )A．x≥0B．-3＜x≤0C．x＞3D．x＞3或x＜0 题目和参考答案——青夏教育精英家教网—

题目内容

20．能使等式$\sqrt{\frac{x}{x-3}}$=$\frac{\sqrt{x}}{\sqrt{x-3}}$成立的条件是（　　）

A．

x≥0

B．

-3＜x≤0

C．

x＞3

D．

x＞3或x＜0

分析利用二次根式的性质得出x≥0，x-3＞0，进而求出即可．

解答解：∵$\sqrt{\frac{x}{x-3}}$=$\frac{\sqrt{x}}{\sqrt{x-3}}$成立，
∴x≥0，x-3＞0，
解得：x＞3．
故选：C．

点评此题主要考查了二次根式的性质，正确利用二次根式的性质求出是解题关键．

练习册系列答案

相关题目

10．

已知：如图，在△ABC中，∠ABC、∠ACB的平分线相交于I，求证：∠BIC=90°+$\frac{1}{2}$∠A．

11．

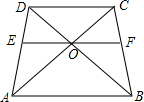在梯形ABCD中，CD∥AB，AC、BD交于点O，过点O作AB的平行线交AD于点E，交BC于点F，则图中有5对相似形三角形；若DC=9，AB=15，则OD：OB=$\frac{3}{5}$，EF=$\frac{45}{4}$．

8．若方程3x²-ax+2b=0的两根和为4，积为-2，则a，b分别为（　　）

15．为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分学生成绩（得分数取正整数，满分为100分）进行统计，绘制统计图如下（未完成），解答下列问题：
（1）若A组的频数比B组小24，求频数分布直方图中的a、b的值；
（2）扇形统计图中，D部分所对的圆心角为n°，求n的值并补全频数分布直方图；
（3）若成绩在80分以上优秀，全校共有2000名学生，估计成绩优秀的学生有多少名？

5．我市教育行政部门为了了解七年级学生每学期参加综合实践活动的情况，随机抽样调查了某中学七年级学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图．

请你根据图中提供的信息，回答下列问题：
（1）扇形统计图中a的值是25%，该校七年级学生总数是200人．
（2）活动时间为5天的学生有10人，并补全条形统计图；
（3）如果该市七年级的学生共有2000人，根据以上数据，试估计这2000人中“活动时间不少于4天”的学生有多少人？

12．数轴上表示无理数$\sqrt{28}$的点界于哪两个相邻的整数点之间（　　）

9．分解因式：
（1）81a⁴-16b⁴
（2）50n-20n（x-y）+2n（x-y）²
（3）1-x²-y²+2xy．

10．在平面直角坐标系xOy中，对于点P（x，y），我们把点P′（-y+1，x+1）叫做点P伴随点．已知点A₁的伴随点为A₂，点A₂的伴随点为A₃，点A₃的伴随点为A₄，…，这样依次得到点A₁，A₂，A₃，…，A_n，…．若点A₁的坐标为（3，1），则点A₃的坐标为（-3，1），点A₂₀₁₅的坐标为（-3，1）．

试题分类