题目内容
11.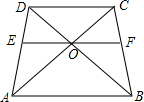 在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.
在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.
分析 由在梯形ABCD中,AB∥CD,于是得到∠ABO=∠CDO,∠OAB=∠DCO,证得△AOB∽△COD,由于EF∥AB,AB∥CD,推出△AEO∽△ACD,△BOF∽△BDC,△DEO∽△DAB,△CFO∽△CAB,得到比例式即可得到结果.
解答 解:∵在梯形ABCD中,AB∥CD,
∴∠ABO=∠CDO,∠OAB=∠DCO,
∴△AOB∽△COD,
∵EF∥AB,AB∥CD,
∴EF∥AB∥CD,
∴△AEO∽△ACD,△BOF∽△BDC,△DEO∽△DAB,△CFO∽△CAB
∴共有5对相似三角形,
∵△AOB∽△COD,△DEO∽△DAB,△CFO∽△CAB,
∴$\frac{OC}{OA}$=$\frac{OD}{OB}=\frac{CD}{AB}=\frac{9}{15}=\frac{3}{5}$,
$\frac{OE}{AB}=\frac{OD}{BD}=\frac{3}{8}$,$\frac{OF}{AB}=\frac{OC}{AC}=\frac{3}{8}$,
∴OE=OF=$\frac{45}{8}$,
∴EF=$\frac{45}{4}$,
故答案为:5,$\frac{3}{5}$,$\frac{45}{4}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
16.父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格.
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面10千米的高空温度是多少吗?
| 距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
| 温度(℃) | 20 | 14 | 8 | 2 | -4 | -10 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面10千米的高空温度是多少吗?
20.能使等式$\sqrt{\frac{x}{x-3}}$=$\frac{\sqrt{x}}{\sqrt{x-3}}$成立的条件是( )
| A. | x≥0 | B. | -3<x≤0 | C. | x>3 | D. | x>3或x<0 |
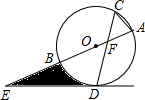 如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.
如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.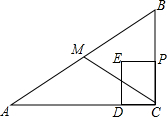 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).