题目内容
4. 如图,在数轴上有A,B两点,点A在点B的左侧,已知点B对应的数为2,点A对应的数为a.
如图,在数轴上有A,B两点,点A在点B的左侧,已知点B对应的数为2,点A对应的数为a.(1)若a=-3,则线段AB的长为5(直接写出结果);
(2)若点C在线段AB之间,且AC-BC=2,求点C表示的数(用含a的式子表示).
分析 (1)根据点A、B表示的数利用两点间的距离公式即可求出AB的长度;
(2)设点C表示的数为x,则AC=x-a,BC=2-x,根据AC-BC=2,即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)AB=2-(-3)=5.
故答案为:5.
(2)设点C表示的数为x,则AC=x-a,BC=2-x,
∵AC-BC=x-a-(2-x)=2,
∴x=2+$\frac{a}{2}$.
∴点C表示的数为2+$\frac{a}{2}$.
点评 本题考查了数轴.两点间的距离以及一元一次方程的应用,解题的关键是:(1)根据点A、B表示的数利用两点间的距离公式求出AB的长度;(2)根据两点间的距离公式结合AC-BC=2列出关于x的一元一次方程.

练习册系列答案
相关题目
9.等腰三角形ABC中,AB=CB=5,AC=8,P为AC边上一动点,PQ⊥AC,PQ与△ABC的腰交于点Q,连结CQ,设AP为x,△CPQ面积为y,则y关于x的函数关系的图象大致是( )
| A. | 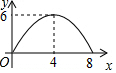 | B. | 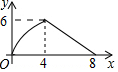 | C. | 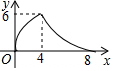 | D. | 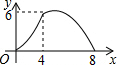 |
16.如果将抛物线y=x2+2先向左平移1个单位,再向下平移2个单位,那么所得新抛物线的表达式是( )
| A. | y=(x-1)2 | B. | y=(x+1)2 | C. | y=x2+1 | D. | y=x2+3 |
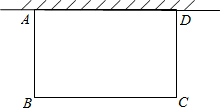 在广元市开展的“双创”活动中,某居民小区要在一块靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园一边靠墙,另三边总长为40m的栅栏(如图所示).当BC的长为多少米时,矩形ABCD的面积为168m2?
在广元市开展的“双创”活动中,某居民小区要在一块靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园一边靠墙,另三边总长为40m的栅栏(如图所示).当BC的长为多少米时,矩形ABCD的面积为168m2?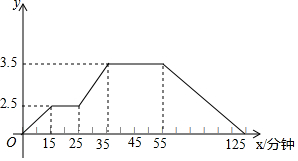 如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.