题目内容
15.(1)若关于a,b的多项式3(a2-2ab-b2)-(a2+mab+2b2)中不含有ab项,求m的值.(2)有一道题,求3a2-4a2b+3ab+4a2b-ab+a2-2ab的值,其中a=-1,b=$\frac{1}{2}$,小明同学把b=$\frac{1}{2}$错写成了b=-$\frac{1}{2}$,但他计算的结果是正确的,请你通过计算说明这是怎么回事?
分析 (1)原式去括号合并得到最简结果,由结果不含ab项确定出m的值;
(2)原式合并同类项得到最简结果,即可作出判断.
解答 解:(1)原式=3a2-6ab-3b2-a2-mab-2b2=2a2-(m+6)ab-5b2,
由结果不含ab项,得到m+6=0,
解得:m=-6;
(2)原式=4a2,
结果与b的取值无关,故小明同学把b=$\frac{1}{2}$错写成了b=-$\frac{1}{2}$,但他计算的结果是正确的.
点评 此题考查了整式的加减-化简求值,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
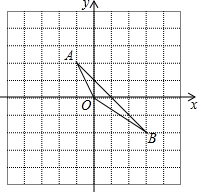 已知点A、B在平面直角坐标系中的位置如图所示,将△AOB向下平移2个单位长度,在向左平移2个单位.
已知点A、B在平面直角坐标系中的位置如图所示,将△AOB向下平移2个单位长度,在向左平移2个单位. 如图,在数轴上有A,B两点,点A在点B的左侧,已知点B对应的数为2,点A对应的数为a.
如图,在数轴上有A,B两点,点A在点B的左侧,已知点B对应的数为2,点A对应的数为a.