题目内容
5.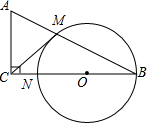 如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.
如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.(1)求证:BA•BM=BC•BN;
(2)如果CM是⊙O的切线,且M为AB的中点,当BN=4时,求MN的长.
分析 (1)连接MN,根据三角形相似的判定方法,判断出△ABC∽△NBM,即可判断出BA•BM=BC•BN;
(2)连接MO、MN,根据直角三角形的性质得到MC=MB,得到∠MCB=∠B,根据弦切角定理证明∠NMC=∠B,得到∠MNO=60°,根据等边三角形的性质得到答案.
解答 (1)证明:如图1,连接MN,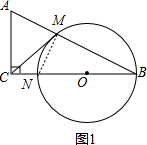
∵NB是⊙O的直径,
∴∠NMB=90°,
在△ABC和△NBM中,
$\left\{\begin{array}{l}{∠ABC=∠NBM}\\{∠ACB=∠NMB}\end{array}\right.$,
∴△ABC∽△NBM,
∴$\frac{BA}{BN}=\frac{BC}{BM}$,
∴BA•BM=BC•BN;
(2)如图2,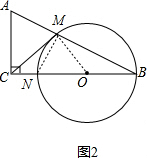 连接MO、MN,
连接MO、MN,
∵∠ACB=90°,M为AB的中点,
∴MC=MB,
∴∠MCB=∠B,
∵CM是⊙O的切线,
∴∠NMC=∠B,
∵∠MNB=∠NCM+∠NMC,
∴∠MNB=2∠B,
∵BN为⊙O的直径,
∴∠NMB=90°,
∴∠MNO=60°,
∴△MNO是等边三角形,
∴MN=2.
点评 本题考查的是切线的性质、相似三角形的判定和性质、三角形的外角的性质、弦切角定理以及等边三角形的判定,正确作出辅助线、灵活运用定理是解题的关键.

练习册系列答案
相关题目
17.下列说法中正确的是( )
| A. | 过一点有且只有一条直线平行于已知直线 | |
| B. | 两条直线被第三直线所截,同位角相等 | |
| C. | 两条直线有两种位置关系:平行、相交 | |
| D. | 同一平面内,垂直于同一条直线的两条直线平行 |
 如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推.
如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推. 已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.
已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.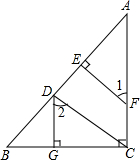 如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.
如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.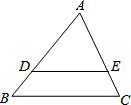 如图,已知DE∥BC,AD=5,DB=3,DE=4,则BC=$\frac{32}{5}$.
如图,已知DE∥BC,AD=5,DB=3,DE=4,则BC=$\frac{32}{5}$.