题目内容
10.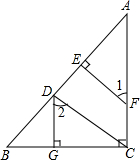 如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.
如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.解:∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠BCA=90°(垂直的定义)
∴DG∥AC
∴∠2=∠DCA
∵∠1=∠2 ( 已知 )
∴∠1=∠DCA
∴EF∥DC
∴∠AEF=∠ADC(两直线平行,同位角相等 )
∵EF⊥AB(已知)
∴∠AEF=90°(垂直定义)
∴∠ADC=90°(等量代换 )
即:CD⊥AB.
分析 根据平行线的判定推出DG∥AC,根据平行线的性质得出∠2=∠DCA,求出∠1=∠DCA,根据平行线的判定得出EF∥DC,根据平行线的性质得出∠AEF=∠ADC即可.
解答 解:∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠BCA=90°(垂直的定义)
∴DG∥AC,
∴∠2=∠DCA,
∵∠1=∠2( 已知 ),
∴∠1=∠DCA,
∴EF∥DC,
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义),
∴∠ADC=90°(等量代换),
即:CD⊥AB,
故答案为:BCA,AC,DCA,∠2,DCA,DC,ADC,两直线平行,同位角相等,(已知),(垂直定义),等量代换.
点评 本题考查了平行线的性质和判定,垂直定义的应用,能灵活运用平行线的性质和判定定理进行推理是解此题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
19.在平面直角坐标系xOy中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转180°,得到OA′,则点A′的坐标是( )
| A. | (-4,3) | B. | (-3,4) | C. | (3,-4) | D. | (-4,-3) |
 如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE、BD、CE相交于点F,且∠ADB=∠BAC.求证:四边形ABFE为菱形.
如图,在△ABC中,AB=AC,将△ABC绕点A逆时针旋转得到△ADE,连接BD、CE、BD、CE相交于点F,且∠ADB=∠BAC.求证:四边形ABFE为菱形.
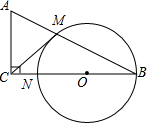 如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.
如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.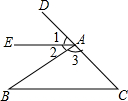 如图,∠1与∠C是两条直线AE、BC被第三条直线CD所截构成的同位角;∠2与∠B是两条直线AE、BC被第三条直线CD所截构成的内错角;∠B与∠C是AB、AC被第三条直线BC所截构成的同旁内角.
如图,∠1与∠C是两条直线AE、BC被第三条直线CD所截构成的同位角;∠2与∠B是两条直线AE、BC被第三条直线CD所截构成的内错角;∠B与∠C是AB、AC被第三条直线BC所截构成的同旁内角.