题目内容
20.已知x2+(m+1)x+2m=0的两根为x1,x2 ,若-1<x1<x2 <1,求m的取值范围.分析 构造函数y=x2+(m+1)x+2m,若-1<x1<x2 <1,则△>0,当x=-1时,y>0,当x=1时,y>0,解不等式组即可.
解答 解:构造函数y=x2+(m+1)x+2m,
∵x2+(m+1)x+2m=0的两根为x1,x2 ,
∴△=(m+1)2-8m=m2-6m+1>0,
解得:m<3-2$\sqrt{2}$或m>3+2$\sqrt{2}$,
若-1<x1<x2 <1,则当x=-1时,y>0,当x=1时,y>0,
即$\left\{\begin{array}{l}{m>0}\\{3m+2>0}\end{array}\right.$,
解得:m>0.
∴0<m<3-2$\sqrt{2}$.
点评 本题考查了抛物线与x轴的交点、一元二次不等式与二次函数的关系以及一元二次方程根与系数的关系,把方程问题和函数图象结合是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若二次函数y=7x2-7x+m的图象与x轴有交点,则m的取值范围是( )
| A. | m$>\frac{7}{4}$ | B. | m$≥\frac{7}{4}$ | C. | m$<\frac{7}{4}$ | D. | m$≤\frac{7}{4}$ |
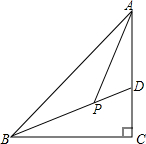 如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由.
如图,在△ABC中,∠C=90°,BD平分∠ABC且交AC于D,点P在BD上,且∠APB=135°,AP是∠BAC的平分线吗?说明理由. 如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.
如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.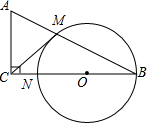 如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.
如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.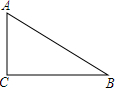 如图,已知△ABC中,∠C=90°,AC=3,BC=4,已点C为圆心作⊙C,半径为r.
如图,已知△ABC中,∠C=90°,AC=3,BC=4,已点C为圆心作⊙C,半径为r.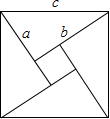 勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.
勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.