题目内容
17.某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k棵树种植在点Pk(xk,yk)处,其中x1=1,y1=1,当k≥2时,$\left\{\begin{array}{l}{x_k}={x_{k-1}}+1-5([\frac{k-1}{5}]-[\frac{k-2}{5}])\\{y_k}={y_{k-1}}+[\frac{k-1}{5}]-[\frac{k-2}{5}]\end{array}\right.$,[a]表示非负实数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2011棵树种植点的坐标为(1,403).分析 根据规律找出种植点的横坐标与纵坐标的通式,然后再把2010代入进行计算即可求解.
解答 解:根据题意,x1=1,
x2-x1=1-5[$\frac{1}{5}$]+5[$\frac{0}{5}$],
x3-x2=1-5[$\frac{2}{5}$]+5[$\frac{1}{5}$],
x4-x3=1-5[$\frac{3}{5}$]+5[$\frac{2}{5}$],
…
xk-xk-1=1-5[$\frac{k-1}{5}$]+5[$\frac{k-2}{5}$],
∴x1+(x2-x1)+(x3-x2)+(x4-x3)+…+(xk-xk-1),
=1+(1-5[$\frac{1}{5}$]+5[$\frac{0}{5}$])+(1-5[$\frac{2}{5}$]+5[$\frac{1}{5}$])+(1-5[$\frac{3}{5}$]+5[$\frac{2}{5}$])+…+(1-5[$\frac{k-1}{5}$]+5[$\frac{k-2}{5}$]),
∴xk=k-5[$\frac{k-1}{5}$],
当k=2011时,x2011=2011-5[$\frac{2010}{5}$]=2011-5×402=1,
y1=1,
y2-y1=[$\frac{1}{5}$]-[$\frac{0}{5}$],
y3-y2=[$\frac{2}{5}$]-[$\frac{1}{5}$],
y4-y3=[$\frac{3}{5}$]-[$\frac{2}{5}$],
…
yk-yk-1=[$\frac{k-1}{5}$]-[$\frac{k-2}{5}$],
∴yk=1+[$\frac{k-1}{5}$],
当k=2011时,y2011=1+[$\frac{2010}{5}$]=1+402=403,
∴第2011棵树种植点的坐标为(1,403).
故答案为:(1,403).
点评 本题考查了坐标位置的确定,根据题目条件找出横坐标与纵坐标的通项公式是解题的关键,规律性较强,难度较大.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
| A. | 25 | B. | 125 | C. | 625 | D. | 512 |
| A. | $(-\right.2,2\sqrt{3}\left.{\;})$ | B. | $(-2,-2\sqrt{3})$ | C. | (2$\sqrt{3}$,2) | D. | (2,2) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
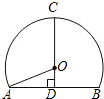 如图,若它的形状是以O为圆心的圆的一部分,AB=8,高CD=8,则半径OA等于5.
如图,若它的形状是以O为圆心的圆的一部分,AB=8,高CD=8,则半径OA等于5.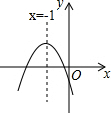 y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:abc,b2-4ac,a-b+c,a+b+c,2a-b,9a-4b中,值大于0的有( )
y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:abc,b2-4ac,a-b+c,a+b+c,2a-b,9a-4b中,值大于0的有( )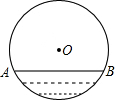 如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,求油的最大深度.
如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,求油的最大深度.