题目内容
9.直角三角形的两条直角边长分别为6cm和8cm,那么这个三角形的外接圆的半径等于5cm,内切圆的半径等于1cm.分析 先利用勾股定理计算出斜边为10cm,再根据直角三角形的斜边等于其外接圆的直径可得这个三角形的外接圆的半径,利用内切圆半径r=$\frac{a+b-c}{2}$(a、b为直角边,c为斜边)易得这个三角形的内切圆的半径.
解答 解:直角三角形的斜边=$\sqrt{{6}^{2}+{8}^{2}}$=10cm,
所以这个三角形的外接圆的半径=$\frac{1}{2}$×10=5(cm),
这个三角形的内切圆的半径=$\frac{6+8-10}{2}$=1(cm).
故答案为5cm,1cm.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心;三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了三角形的外心性质.记住直角三角形的外接圆半径R=$\frac{c}{2}$,内切圆半径r=$\frac{a+b-c}{2}$(a、b为直角边,c为斜边).

练习册系列答案
相关题目
19.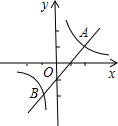 如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )
如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )
 如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )
如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )| A. | x>2 | B. | -1<x<0或x>2 | C. | -1<x<2 | D. | x<-1或x>2 |
14. 如图,把正方形ABCD的对角线AC分成n段,以每一段为对角线作正方形,设这n个小正方形的周长和为p,正方形ABCD的周长为S,则S与p的关系( )
如图,把正方形ABCD的对角线AC分成n段,以每一段为对角线作正方形,设这n个小正方形的周长和为p,正方形ABCD的周长为S,则S与p的关系( )
 如图,把正方形ABCD的对角线AC分成n段,以每一段为对角线作正方形,设这n个小正方形的周长和为p,正方形ABCD的周长为S,则S与p的关系( )
如图,把正方形ABCD的对角线AC分成n段,以每一段为对角线作正方形,设这n个小正方形的周长和为p,正方形ABCD的周长为S,则S与p的关系( )| A. | S<p | B. | S>p | C. | S=p | D. | S与p无关 |
19.分式$\frac{{x}^{2}-9}{x+3}$的值为0,则( )
| A. | x=-3 | B. | x=±3 | C. | x=3 | D. | x=0 |
 如图,已知AB=AC,DE=DF,求证:BE=CF.
如图,已知AB=AC,DE=DF,求证:BE=CF. .
.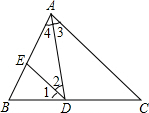 请在括号里填上推理的根据
请在括号里填上推理的根据