Question

5．如图（1），已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A₁B₁C₁D₁；把正方形A₁B₁C₁D₁边长按原法延长一倍后得到正方形A₂B₂C₂D₂（如图（2））；以此下去…，则正方形A₄B₄C₄D₄的面积为（　　）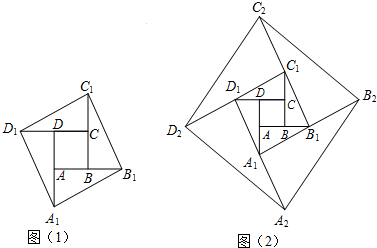

• A． 25
• B． 125
• C． 625
• D． 512

Answer 1

分析 连结AC，B₁C，如图（1），根据三角形面积公式得到S_△ABC=S_△BB1C，S_△BB1C=S_△CC1B1，则S_△BB1C=2S_△ABC=S_{正方形ABCD}=1，所以S_{正方形A1B1C1D1}=5S_{正方形ABCD}=5，同理可得S_{正方形A2B2C2D2}=5S_{正方形A1B1C1D1}=5²，按照此规律易得正方形A₄B₄C₄D₄的面积．

解答 解：连结AC，B₁C，如图（1），
∵AB=BB₁，BC=CC₁，
∴S_△ABC=S_△BB1C，S_△BB1C=S_△CC1B1，
∴S_△BB1C=2S_△ABC=S_{正方形ABCD}=1，
∴S_{正方形A1B1C1D1}=5S_{正方形ABCD}=5，
同理可得S_{正方形A2B2C2D2}=5S_{正方形A1B1C1D1}=5²，
∴正方形A₄B₄C₄D₄的面积=5⁴=625．
故选C．

点评 本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质．两条对角线将正方形分成四个全等的等腰直角三角形．也考查了规律型问题的解决方法．