题目内容
1.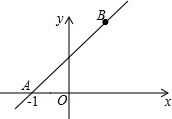 如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).
如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).
分析 本题本题可先根据三角函数求出AC和BC的值,由此即可得出B点的坐标.
解答 解:∵∠BAC=45°,∠BCA=90°,AB=2$\sqrt{2}$,
则AC=BC=2,
∴点B的横坐标为1,纵坐标为2.
故答案为:(1,2)
点评 本题主要考查了三角函数的应用,关键是根据三角函数求出AC和BC的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.画出圆柱从正面,左面,上面看到的形状图
| 图形 | 从正面看 | 从左面看 | 从上面看 |
 |
13.下列因式分解正确的是( )
| A. | -a+a3=-a(1+a2) | B. | 2a-4b+2=2(a-2b) | C. | a2-2a+1=(a-1)2 | D. | a2-4=(a-2)2 |
10. 如图,为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12m,那么A、B间的距离不可能是( )
如图,为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12m,那么A、B间的距离不可能是( )
 如图,为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12m,那么A、B间的距离不可能是( )
如图,为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12m,那么A、B间的距离不可能是( )| A. | 10m | B. | 15m | C. | 20m | D. | 29m |
11.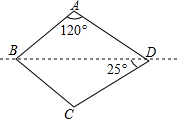 如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )
如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )
 如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )
如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 80° |
 如图,已知直线AB和CD相交于O点,OE⊥CD,垂足为O点,OF平分∠AOE,且∠AOE=112°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,OE⊥CD,垂足为O点,OF平分∠AOE,且∠AOE=112°,求∠COF的度数.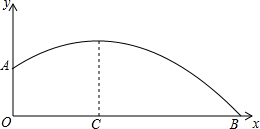 一男生掷铅球,铅球行进的高度y(m)与水平距离x(m)之前的函数关系是:y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$.函数的图象如图所示,观察图象,计算出铅球掷出的最大高度和距离(即OB的长)
一男生掷铅球,铅球行进的高度y(m)与水平距离x(m)之前的函数关系是:y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$.函数的图象如图所示,观察图象,计算出铅球掷出的最大高度和距离(即OB的长)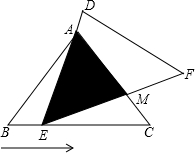 如图,在△ABC中,已知AB=AC=3,BC=4,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF交于AC于M点.
如图,在△ABC中,已知AB=AC=3,BC=4,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF交于AC于M点.