题目内容
11. 如图,已知直线AB和CD相交于O点,OE⊥CD,垂足为O点,OF平分∠AOE,且∠AOE=112°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,OE⊥CD,垂足为O点,OF平分∠AOE,且∠AOE=112°,求∠COF的度数.
分析 由垂线的定义可知:∠COE=90°,然后根据角平分线的定义可知∠EOF=56°,最后依据∠COF=∠COE-∠EOF求解即可.
解答 解:∵OE⊥CD,
∴∠COE=90°.
∵OF 平分∠AOE,
∴∠EOF=$\frac{1}{2}$∠AOE=56°.
∴∠COF=∠COE-∠EOF=90°-56°=34°.
点评 本题主要考查的是角平分线的性质、垂线的定义、角的和差计算,求得∠EOF=56°是解题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
1.若$\sqrt{{a}^{2}}$=-a,则正确的是( )
| A. | a>0 | B. | a≥0 | C. | a<0 | D. | a≤0 |
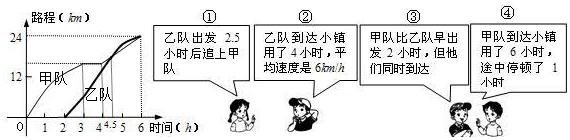
19.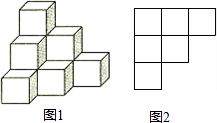 下面说法错误的是( )
下面说法错误的是( )
 下面说法错误的是( )
下面说法错误的是( )| A. | 一个平面截一个球,得到的截面一定是圆 | |
| B. | 一个平面截一个正方体,得到的截面可以是五边形 | |
| C. | 图2是几何体图1的左视图 | |
| D. | 棱柱的截面不可能是圆 |
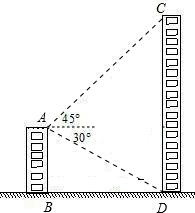 如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).
如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).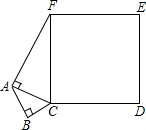 如图,BC=3,AB=4,AF=12,∠FAC和∠ABC都为直角,求正方形FCDE的面积.
如图,BC=3,AB=4,AF=12,∠FAC和∠ABC都为直角,求正方形FCDE的面积.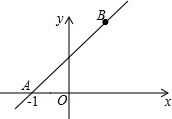 如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).
如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).