题目内容
12.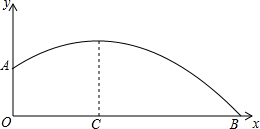 一男生掷铅球,铅球行进的高度y(m)与水平距离x(m)之前的函数关系是:y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$.函数的图象如图所示,观察图象,计算出铅球掷出的最大高度和距离(即OB的长)
一男生掷铅球,铅球行进的高度y(m)与水平距离x(m)之前的函数关系是:y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$.函数的图象如图所示,观察图象,计算出铅球掷出的最大高度和距离(即OB的长)
分析 求铅球掷出的最大高度即为求出函数y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$的顶点坐标的纵坐标;求铅球推出的距离即函数y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$的图象和横轴在正半轴的交点,令函数值y=0,解一元二次方程即可.
解答 解:∵y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$,
∴$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-\frac{1}{12})×\frac{5}{3}-(\frac{2}{3})^{2}}{4×(-\frac{1}{12})}$=3,
∴铅球掷出的最大高度为3m,
令y=0,
∴0=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$,
∴x2-8x-20=0
解得:x1=10,x2=-2(舍去)
∴铅球推出的距离是10米.
点评 本题考查了二次函数在实际问题的应用,当y=0时可求出图形和横轴的交点坐标,顶点坐标的纵坐标即为铅球掷出的最大高度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.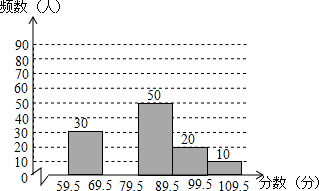 某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:
某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:
请根据以上图表提供的信息,解答下列问题:
(1)填写表格中的空格,并补全频数分布直方图;
(2)所抽取部分参赛同学的成绩的中位数落在第第二组;
(3)如果比赛成绩90分以上(含90分)可以获得奖励,该校共有600人参加比赛,估计该校约有多少人可以获得.
 某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:
某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:| 分数段 | 频数 | 频率 |
| 第一次:59.5-69.5 | 30 | 0.15 |
| 第二次:69.5-79.5 | 90 | 0.45 |
| 第三次79.5-89.5 | 50 | 0.25 |
| 第四组89.5-99.5 | 20 | 0.1 |
| 第五组99.5-109.5 | 10 | 0.05 |
(1)填写表格中的空格,并补全频数分布直方图;
(2)所抽取部分参赛同学的成绩的中位数落在第第二组;
(3)如果比赛成绩90分以上(含90分)可以获得奖励,该校共有600人参加比赛,估计该校约有多少人可以获得.
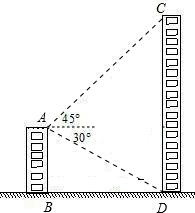 如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).
如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).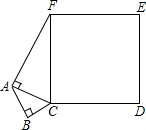 如图,BC=3,AB=4,AF=12,∠FAC和∠ABC都为直角,求正方形FCDE的面积.
如图,BC=3,AB=4,AF=12,∠FAC和∠ABC都为直角,求正方形FCDE的面积. 如图,一个刷成黑白色且能折成长方体的模型,由它折成的长方体是下列图形中的哪一个( )
如图,一个刷成黑白色且能折成长方体的模型,由它折成的长方体是下列图形中的哪一个( )



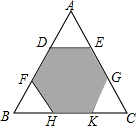 如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小三角形这边长是多少.
如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小三角形这边长是多少.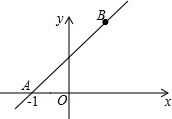 如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).
如图,在平面直角坐标系中,直线AB与x轴的夹角为45°,点A的坐标为(-1,0),点B在y轴右侧,设AB=2$\sqrt{2}$,那么点B的坐标为(1,2).