题目内容
7.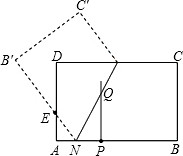 如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点,折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( )
如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点,折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( )| A. | 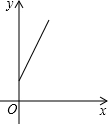 | B. | 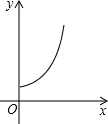 | C. |  | D. | 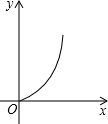 |
分析 过点E作EF⊥QP,垂足为F,连接EQ.由翻折的性质可知QE=QP,从而可表示出QF、EF、EQ的长度,然后在△EFQ中利用勾股定理可得到函数的关系式.
解答 解:如图所示,过点E作EF⊥QP,垂足为F,连接EQ.
由翻折的性质可知:EQ=QP=y.
∵∠EAP=∠APF=∠PFE=90°,
∴四边形EAPF是矩形.
∴EF=AP=x,PF=EA=1.
∴QF=QP-PF=y-1.
在Rt△EFQ中,由勾股定理可知:EQ2=QF2+EF2,即y2=(y-1)2+x2.
整理得:y=$\frac{1}{2}{x}^{2}+\frac{1}{2}$.
故选:B.
点评 本题主要考查的是翻折的性质、矩形的性质和判定、勾股定理的应用,表示出QF、EF、EQ的长度,在△EFQ中利用勾股定理列出函数关系式是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
19.张先生在上周五(周六周日不开盘)买进了某公司的股票1000股,每股28元.下表是本周每天股票的涨跌情况(单位:元)
求:(1)本周星期三收盘时,每股是多少元?
(2)本周内最高价每股多少元?最低价每股多少元?
(3)已知张先生买进股票时付了0.1%的手续费,卖出时需交了手续费和个人所得税共0.3%,如果张先生在本周末收盘时把全部股票卖出,他的收益是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌/元 | +2.8 | +3 | -2 | +1.5 | -2.5 |
(2)本周内最高价每股多少元?最低价每股多少元?
(3)已知张先生买进股票时付了0.1%的手续费,卖出时需交了手续费和个人所得税共0.3%,如果张先生在本周末收盘时把全部股票卖出,他的收益是多少元?
16.如果把分式$\frac{ab}{a+b}$中a,b都扩大3倍,那么分式的值一定( )
| A. | 不变 | B. | 是原来的$\frac{1}{3}$ | C. | 是原来的3倍 | D. | 是原来的9倍 |

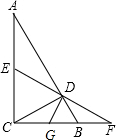 如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴上一点,且sin∠AOE=$\frac{4}{5}$.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴上一点,且sin∠AOE=$\frac{4}{5}$.