题目内容
18．在Rt△ABC中，∠C=90°，AC=3，BC=4，以A为圆心，R为半径画⊙A，使点C在⊙A的内部，点B在⊙A的外部，那么半径R应满足的条件是3＜R＜5．分析 若使点C在⊙A的内部，则所画圆的半径R＞AC，若使点B在⊙A的外部，则所画圆的半径R＜AB，由此可得到半径R应满足的条件．
解答 
解：以A为圆心，R为半径画⊙A，使点C在⊙A的内部，则所画圆的半径R＞AC，即R＞3，
若点B在⊙A的外部，则所画圆的半径R＜AB，即R＜5，
故答案为：3＜R＜5．
点评 本题考查了对点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
练习册系列答案
阅读快车系列答案
相关题目
8．实数-$\frac{1}{2}$的绝对值是（ ）
| A． | 2 | B． | -2 | C． | -|$\frac{1}{2}$| | D． | $\frac{1}{2}$ |
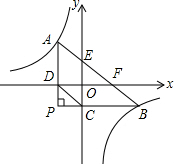如图，Rt△ABC的直角顶点P落在第三象限内，顶点A，B分别落在反比例函数y=$\frac{k}{x}$图象的两支上，且PA⊥x轴于点D，PB⊥y轴于点C，AB分别与x轴、y轴相交于点F、E，已知B（3，-1）．
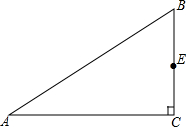已知，如图，△ABC中，∠C=90°，E为BC边中点．
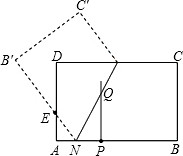如图，矩形纸片ABCD中，AB=5，BC=3，点E在AD上，且AE=1，点P是线段AB上一动点，折叠纸片，使点P与点E重合，展开纸片得折痕MN，过点P作PQ⊥AB，交MN所在的直线于点Q．设x=AP，y=PQ，则y关于x的函数图象大致为（ ）
