题目内容
15.如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数y=$\frac{k}{x}$(k>0)在第一象限内的图象经过点A(6,8),与BC交于点F.
(1)求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=36,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
分析 (1)把A点坐标代入反比例函数中,求出k的值,即可求出反比例函数的解析式;
(2)根据平行四边形的中位线,可得E点的坐标,根据EF平行于x轴,可得F点的纵坐标,根据自变量与函数值的对应关系,可得F点的坐标,根据两点间距离公式,可得EF的长,根据AC的长与EF长的关系,可得C点坐标,根据勾股定理,可得OA的长;
(3)分类讨论:当OA=OP=10时,当AP=OA=10时,当PA=OP时,根据两点间距离公式,可得关于x的方程,根据解方程,可得P点坐标.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$(k>0)在第一象限内的图象经过点A(6,8),
∴k=6×8=48,
∴反比例函数解析式为:y=$\frac{48}{x}$;
(2)由F是BC的中点,EF∥OB,得
E是OA的中点,E的横坐标为$\frac{0+6}{2}$=3,纵坐标为$\frac{0+8}{2}$=4,即E(3,4).
F的纵坐标为4,当y=4时,4=$\frac{48}{x}$,解得x=12,F(12,4),
EF=12-3=9,
AC=EF=6+9=15,
AC∥OB,
C(15,8);
由勾股定理,得AO=$\sqrt{{6}^{2}+{8}^{2}}$=10;
(3)设P(x,4),当OA=OP=10时,x2+42=102,解得x=±2$\sqrt{21}$,P1(2$\sqrt{21}$,4),P2(-2$\sqrt{21}$,4);
当AP=OA=10时,(x-6)2+(4-8)2=102,解得x=6±$\sqrt{59}$,P3(6+$\sqrt{59}$,4),P4(6-$\sqrt{59}$,4);
当PA=OP时,(x-6)2+(4-8)2=x2+42,解得x=3,P5(3,4);
综上所述,P1(2$\sqrt{21}$,4),P2(-2$\sqrt{21}$,4);P3(6+$\sqrt{59}$,4),P4(6-$\sqrt{59}$,4);P5(3,4)时,以P、O、A为顶点的三角形是等腰三角形.
点评 本题考查了反比例函数综合题,利用了待定系数法求函数解析式,平行四边形中位线的性质,勾股定理,等腰三角形的判定,分类讨论是解题关键,以防遗漏.

| A. | 1<m<3 | B. | 1≤m<2或2<m<3 | C. | m<1 | D. | m>3 |
| A. | 14 | B. | 20 | C. | 24 | D. | 48 |
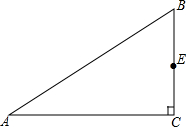 已知,如图,△ABC中,∠C=90°,E为BC边中点.
已知,如图,△ABC中,∠C=90°,E为BC边中点.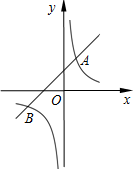 如图,已知一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2).
如图,已知一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2).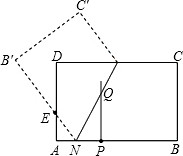 如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点,折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( )
如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD上,且AE=1,点P是线段AB上一动点,折叠纸片,使点P与点E重合,展开纸片得折痕MN,过点P作PQ⊥AB,交MN所在的直线于点Q.设x=AP,y=PQ,则y关于x的函数图象大致为( )