Question

9．已知△ABC，点F在射线CA上，点E在射线AB上，点D在射线CB上，点F、E、D在同一条直钱上，且∠AFE=∠BED．
（1）当BD=DC时，如图①，求证：BE=CF；
（2）当BD：DC=2：3时，如图②、③，BE、CF有怎样的数量关系？请直接写出你的猜想结论，不需要证明；
（3）若BD：DC=1：2，CF=10，AB=8，则AE=13．

Answer 1

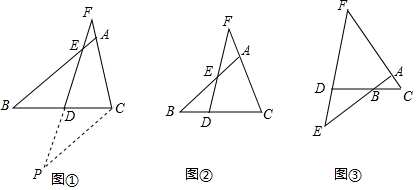
分析 （1）作CP∥AB交FD的延长线于P，则∠P=∠BED，再由已知条件得出∠P=∠AFE，证出CP=CF，由AAS证明△BDE≌△CDP，得出BE=CP，即可得出结论；
（2）作CP∥AB交FD的延长线于P，同（1）得：CP=CF，由平行线证出△BDE∽△CDP，得出对应边成比例BE：CP=BD：CD=2：3，即可得出结论；
（3）作CP∥AB交FD的延长线于P，则∠P=∠BED=∠AFE，由等腰三角形的判定定理得出CP=CF=10，由平行线证出△BDE∽△CDP，得出BE：CP=BD：DC=1：2，求出BE=$\frac{1}{2}$CP=5，即可得出结果．

解答 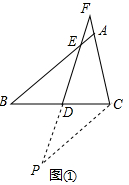（1）证明：作CP∥AB交FD的延长线于P，如图①所示：
则∠P=∠BED，
∵∠AFE=∠BED，
∴∠P=∠AFE，
∴CP=CF，
在△BDE和△CDP中，$\left\{\begin{array}{l}{∠BED=∠P}&{\;}\\{∠BDE=∠CDP}&{\;}\\{BD=CD}&{\;}\end{array}\right.$，
∴△BDE≌△CDP（AAS），
∴BE=CP，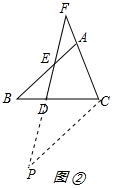
∴BE=CF；
（2）解：BE：CF=2：3，理由如下：
作CP∥AB交FD的延长线于P，如图②所示：
同（1）得：CP=CF，
∵CP∥AB，
∴△BDE∽△CDP，
∴BE：CP=BD：CD=2：3，
∴BE：CF=2：3；
（3）解：作CP∥AB交FD的延长线于P，如图③所示：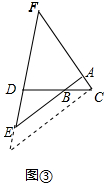
则∠P=∠BED=∠AFE，
∴CP=CF=10，
∵CP∥AB，
∴△BDE∽△CDP，
∴BE：CP=BD：DC=1：2，
∴BE=$\frac{1}{2}$CP=5，
∴AE=AB+BE=8+5=13；
故答案为：13．

点评 本题是三角形综合题目，考查了等腰三角形的判定、平行线的性质、全等三角形的判定与性质、相似三角形的判定与性质；本题综合性强，有一定难度，通过作平行线证明三角形全等和三角形相似是解决问题的关键．