题目内容
13.如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题.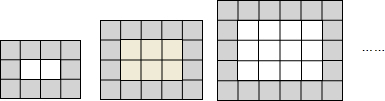
(1)在第n个图中,每一横行共有n+3 块瓷砖,每一竖列共有n+2块瓷砖(用含n的代数式表示);
(2)第n个图中,黑瓷砖有多少块?白瓷砖有多少块?
(3)按上述铺设方案,若铺一块这样的矩形地面共用了黑瓷砖86块,黑瓷砖4元/块,白瓷砖3元/块,则需花多少元购买瓷砖?
分析 (1)先观察图形得出:第1个图形的瓷砖的每行有(1+3)个,每列有(1+2)个;所以第n个图形的瓷砖的每行有(n+3)个,每列有(n+2)个;
(2)首先代入数据期待白色瓷砖的数目,然后用总数减去白色瓷砖的数目即可得到黑色瓷砖的数目.
(3)首先根据总数求得n的值,然后分别求出白瓷砖和黑瓷砖的数量,再进一步计算总价钱;
解答 解:(1)第1个图形的瓷砖的每行有(1+3)个,每列有(1+2)个;
第2个图形的瓷砖的每行有(2+3)个,每列有(2+2)个;
…
∴第n个图形的瓷砖的每行有(n+3)个,每列有(n+2)个;
故答案为:n+3,n+2;
(2)第1个图中有白块瓷砖的块数为:2×1=2块;
第2个图中有白块瓷砖的块数为:3×2=(2+1)×2=6块;
第3个图中有白块瓷砖的块数为:4×3=(3+1)×3=12块;
…
则第n个图中有白块瓷砖的块数为:n(n+1)块;
第1个图形的黑色瓷砖为:3×4-1×2=10块;
第2个图形的黑色瓷砖为:4×5-2×3=14块;
…
则第n个图形的黑色瓷砖为:(n+2)(n+3)-n(n+1)=4n+6块;
答:第n个图中,黑瓷砖有(4n+6)块,白瓷砖有n(n+1)块;
(3)由题意得:4n+6=86,n=20;
当n=20时,白块瓷砖的块数为:n(n+1)=20×21=420;
∴共需花费86×4+420×3=1604(元).
答:则需花1604元购买瓷砖.
点评 本题是图形的变化类规律题,考查了图形的变化问题,解决此题的关键是能够正确结合图形用代数式表示出黑、白瓷砖的数量,再根据题意列方程求解.

练习册系列答案
相关题目
1.如图,已知点E,D,F分别为△ABC三边上的点,下列条件中能判断EF∥BC的是( )
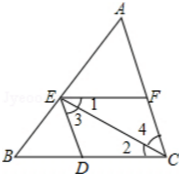

| A. | ∠1=∠3 | B. | ∠3=∠A | C. | ∠1=∠2 | D. | ∠1=∠A |
8.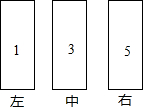 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )| A. | 同样的音“1” | B. | 同样的音“3” | C. | 同样的音“5” | D. | 不同的两个音 |
18.已知点(3,-1)是y=$\frac{k}{x}$(k≠0)双曲线上的一点,则下列各点在该双曲线上的是( )
| A. | (1,3) | B. | (-1,-3) | C. | (-1,3) | D. | (3,1) |
 如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:
如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明: 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.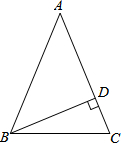 如图,在△ABC中,∠C=∠ABC=$\frac{3}{2}$∠A,BD是边AC上的高.求∠DBC的度数.
如图,在△ABC中,∠C=∠ABC=$\frac{3}{2}$∠A,BD是边AC上的高.求∠DBC的度数.