题目内容
5. 如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:
如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:(1)M为EF的中点;
(2)A、G、E、F四点共圆.
分析 (1)先判断出△HMF∽△FMA即可得出MF2=MH×MA,同理:ME2=MH×MA即可得出结论;
(2)先判断出四边形CENF是平行四边形,进而判断出A、E、N、F四点共圆.,A、G、E、N四点共圆,即可得出A、G、E、N、F五点共圆.得证.
解答 证明:(1)如图,
连结EH、CH、FH.
∴∠FAM=∠DAH=∠DCH,
∵E、C、H、F四点共圆,
∴∠HFM=∠DCH
∴∠HFM=∠FAM,
∴△HMF∽△FMA,
∴$\frac{MF}{MA}=\frac{MH}{MF}$,
∴MF2=MH×MA,
同理:ME2=MH×MA,
∴ME=MF.
∴M为EF的中点;
(2)延长CM到N,使MN=MC,连接EN,FN,AG,EG,
由(1)知,ME=MF,
∴四边形CENF是平行四边形,
∴∠ENF=∠ECF=∠BCD=180°-∠EAF,
∴A、E、N、F四点共圆.,
∵∠GAE=∠GAB=∠GCB=∠FCN=∠ENC=∠ENG,
∴A、G、E、N四点共圆,
∴A、G、E、N、F五点共圆.
∴A、G、E、F四点共圆.
点评 此题是四点共圆,主要考查的四点共圆的性质和判定,相似三角形的性质,平行四边形的性质和判定,圆的性质,解本题的关键是四边形CENF是平行四边形,难点是作出辅助线.是一道难度不大的竞赛常考题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
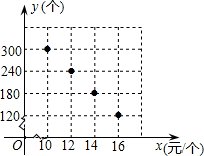 某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示:
某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示:
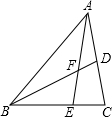 如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示).
如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示).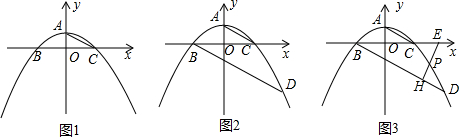

 如图,用扳手拧螺帽,已知正六边形的螺帽的边长为a,当扳手开口的最大值是10cm,求能拧下最大正六边形的螺帽的边长a的值.
如图,用扳手拧螺帽,已知正六边形的螺帽的边长为a,当扳手开口的最大值是10cm,求能拧下最大正六边形的螺帽的边长a的值.