Question

2．如图，四边形ABCD为菱形，对角线AC，BD相交于点E，F是边BA延长线上一点，连接EF，以EF为直径作⊙O，交DC于D，G两点，AD分别与EF，GF交于I，H两点．
（1）求证：AE∥FD；
（2）试判断AF与AB的数量关系，并说明理由；
（3）当G为线段DC的中点时，
①求证：AE=IE；
②若AC=4，求GF的长．

Answer 1

分析 （1）欲证明AE∥DF，只要证明∠BEA=∠BDF=90°即可．
（2）结论：AF=AB，只要证明四边形AFDC是平行四边形，推出AF=CD，由CD=AB，解决问题．
（3）①如图2中，连接GE．欲证明EI=EA，只要证明∠EIA=∠EAI即可．
②在Rt△DEC中，由DG=GC，推出GE=DG=GC，设GE=a，则DC=2a，首先求出EF，△FEG∽△DCE，得$\frac{EG}{CE}$=$\frac{EF}{CD}$，列出方程求出a²，再根据勾股定理即可解决问题．

解答 解：（1）如图1中，

∵四边形ABCD是菱形，
∴AC⊥BD，
∵EF是直径，
∴∠EDF=90°，
∴∠BEA=∠BDF=90°，
∴AE∥DF．

（2）结论：AF=AB．
∵四边形ABCD是菱形，
∴AB=CD，AB∥CD，
∵DF∥AC，
∴四边形AFDC是平行四边形，
∴AF=CD，
∴AF=AB．

（3）①如图2中，连接GE．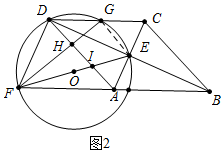

∵EF是直径，
∴∠EGF=90°，
∵DG=GC，EC=AE，
∴GE∥AD，
∴∠EIA=∠FEG，
∵∠ADE+∠DAE=90°，∠GFE+∠FEG=90°，
∵∠CDB=∠BDA=∠EFG，
∴∠DAE=∠FEG，
∴∠DAE=∠EIA，
∴EI=EA．
②在Rt△DEC中，∵DG=GC，
∴GE=DG=GC，设GE=a，则DC=2a，
∵AC=4，AE=EC，
∴EI=EA=2，
∵DF∥AE，
∴∠FDI=∠EAI=∠EIA=∠DIF，
∴DF=IF，由（2）可知DF=AC=4，
∴EF=FI+EI=6，
∵∠EFG=∠CDE，∠FGE=∠DEC=90°，
∴△FEG∽△DCE，
∴$\frac{EG}{CE}$=$\frac{EF}{CD}$，
∴$\frac{a}{2}$=$\frac{6}{2a}$，
∴a²=6，
在Rt△EFG中，FG=$\sqrt{E{F}^{2}-G{E}^{2}}$=$\sqrt{{6}^{2}-6}$=$\sqrt{30}$．

点评 本题考查圆综合题、菱形的性质、平行四边形的判定和性质、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考压轴题．