题目内容
3.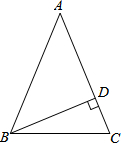 如图,在△ABC中,∠C=∠ABC=$\frac{3}{2}$∠A,BD是边AC上的高.求∠DBC的度数.
如图,在△ABC中,∠C=∠ABC=$\frac{3}{2}$∠A,BD是边AC上的高.求∠DBC的度数.
分析 先设∠A=x,根据三角形内角和定理列出方程,求得x的值,最后根据直角三角形求得∠CBD的 度数.
解答 解:设∠A=x,则∠C=∠ABC=$\frac{3}{2}$x,
∵BD是边AC上的高
∴∠ADB=∠CDB=90°
∴∠ABD=90°-∠A=90°-x
∠CBD=90°-∠C=90°-$\frac{3}{2}$x
∴90°-x+90°-$\frac{3}{2}$x=$\frac{3}{2}$x
解得x=45°
∴∠CBD=90°-∠C=90°-$\frac{3}{2}$x=22.5°
点评 本题主要考查了三角形内角和定理,解决问题的关键是掌握:三角形内角和是180°.解题时注意方程思想的运用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
8.下列说法正确的是( )
| A. | 单项式a的系数是0 | |
| B. | 单项式-$\frac{3xy}{5}$的系数和次数分别是-3和2 | |
| C. | 单项式-3πxy2z3的系数和次数分别是-3π和6 | |
| D. | 3mn与4nm不是同类项 |
12.下列说法错误的是( )
| A. | 2x2-3xy-1是二次三项式 | B. | -x+1是多项式 | ||
| C. | -$\frac{2}{3}$πxy2的系数是-$\frac{2}{3}$π | D. | x与π是同类项 |
 已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.
已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts. 如图,用扳手拧螺帽,已知正六边形的螺帽的边长为a,当扳手开口的最大值是10cm,求能拧下最大正六边形的螺帽的边长a的值.
如图,用扳手拧螺帽,已知正六边形的螺帽的边长为a,当扳手开口的最大值是10cm,求能拧下最大正六边形的螺帽的边长a的值.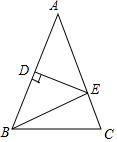 如图,△ABC中,AB=AC,DE垂直平分AB,D为垂足交AC于E.
如图,△ABC中,AB=AC,DE垂直平分AB,D为垂足交AC于E.