题目内容
11. 如图,AB是⊙O的直径,C,D在⊙O上,CD=AD,分别延长CD、BA相交于点E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半径.
如图,AB是⊙O的直径,C,D在⊙O上,CD=AD,分别延长CD、BA相交于点E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半径.
分析 连接AC,OD交于F,由CD=AD,得到$\widehat{CD}$=$\widehat{AD}$,根据垂径定理得到OD⊥AC,AD=CF,根据三角形的中位线的性质得到OF∥BC,根据相似三角形的性质得到$\frac{OD}{BC}=\frac{OE}{BE}$,于是得到结论.
解答 解:连接AC,OD交于F,
∵CD=AD,
∴$\widehat{CD}$=$\widehat{AD}$,
∴OD⊥AC,AD=CF,
∵AO=BO,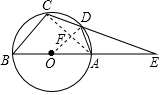
∴OF∥BC,
∵OD∥BC,
∴△ODE∽△BEC,
∴$\frac{OD}{BC}=\frac{OE}{BE}$,
∵AE=$\sqrt{2}$OA,
∴$\frac{OA}{6}=\frac{(1+\sqrt{2})OA}{(2+\sqrt{2})OA}$,
∴OA=3$\sqrt{2}$.
∴⊙O的半径是3$\sqrt{2}$.
点评 本题考查了相似三角形的判定和性质,三角形的中位线的性质,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.2013的相反数是( )
| A. | -2013 | B. | -$\frac{1}{2013}$ | C. | 2013 | D. | $\frac{1}{2013}$ |
1.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:现该工稈队进行人员调整:减少木工2名,增加电工、瓦工各1名:与调整前相比,该工程队员工月工资的方差变大(填“变小”、“不变”或“变大”)
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 5 | 4000 |
| 木工 | 4 | 3000 |
| 瓦工 | 5 | 2000 |
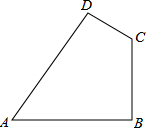 如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.
如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补. 如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF=$\sqrt{39}$.
如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF=$\sqrt{39}$.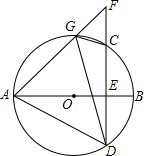 如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( )
如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( )