题目内容
10.先化简式子($\frac{x+2}{{x}^{2}-2x}-\frac{1}{x-2}$)$÷\frac{2}{{x}^{2}-4}$,再任选一个你喜欢且使原式有意义的数代入求值.分析 先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:原式=($\frac{x+2}{x(x-2)}$-$\frac{x}{x(x-2)}$)•$\frac{(x+2)(x-2)}{2}$
=$\frac{2}{x(x-2)}$•$\frac{(x+2)(x-2)}{2}$
=$\frac{x+2}{x}$.
当x=1时,原式=$\frac{1+2}{1}$=3.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
5.若2x=6,2y=3,则2x-2y的值为( )
| A. | 0 | B. | 3 | C. | -3 | D. | $\frac{2}{3}$ |
2.下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图形中白色正方形的个数为( )


| A. | 20 | B. | 30 | C. | 32 | D. | 34 |
 尺规作图:(要求保留作图痕迹,不要求写出作法)
尺规作图:(要求保留作图痕迹,不要求写出作法) 已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC于点E.求证:
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC于点E.求证: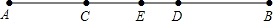 如图,已知AB=10cm,点C在线段AB上,且AC比BC短4cm.
如图,已知AB=10cm,点C在线段AB上,且AC比BC短4cm.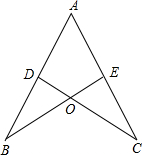 如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O. 如图,阴影部分由哪块图形旋转而成?请在图中标示出来.若大圆半径为3,小圆半径为1,求阴影部分的面积.
如图,阴影部分由哪块图形旋转而成?请在图中标示出来.若大圆半径为3,小圆半径为1,求阴影部分的面积. 如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是4个.
如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是4个.