题目内容
18.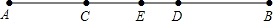 如图,已知AB=10cm,点C在线段AB上,且AC比BC短4cm.
如图,已知AB=10cm,点C在线段AB上,且AC比BC短4cm.(1)求线段AC的长.
(2)若点D、E分别为BC、AB的中点,求线段DE的长.
分析 (1)根据AC比BC短4cm,可用AC表示BC,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得BD的长,BE的长,根据线段的和差,可得答案.
解答 解:(1)由点C在线段AB上,且AC比BC短4cm,得
BC=AC+4,
由线段的和差,得
AC+BC=AB,即AC++AC+4=10,
解得AC=3cm;
(2)BC=AC+4=3+4=7,
由点D、E分别为BC、AB的中点,得
BD=$\frac{1}{2}$BC=$\frac{1}{2}$×7=$\frac{7}{2}$,
BE=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5.
由线段的和差,得
DE=BE-BD=5-$\frac{7}{2}$=$\frac{3}{2}$cm
点评 本题考查了两点间的距离,利用线段的和差得出关于AC方程是解题关键.

练习册系列答案
相关题目
6.用“△”表示一种运算符号,其意义是a△b=2a-b,若x△(-1)=2,则x等于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
3.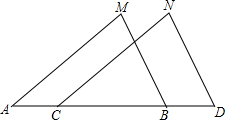 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )| A. | AM=CN | B. | AC=BD | C. | ∠M=∠N | D. | AM∥CN |
8.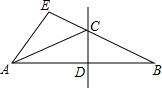 如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )
如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )
 如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )
如图,△ABE中,CD是线段AB的垂直平分线,如果AE=4cm,△ACE的周长为11cm,则BE长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
 如图,是一个正方体表面展开图,请在图中空格内填上适当的数,使这个正方体相对两个面上标注的数值相等(将答案填在图中空格内)
如图,是一个正方体表面展开图,请在图中空格内填上适当的数,使这个正方体相对两个面上标注的数值相等(将答案填在图中空格内)