题目内容
10．一个多边形内角和比四边形的内角和多540度，多边形内角和相等，多边形有几个边（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
分析 首先由题意得出等量关系，即这个多边形的内角和比四边形的内角和多540°，由此列出方程解出边数．
解答 解：设这个多边形的边数为n，则
（n-2）•180°=360°+540°，
解得n=7．
故选：B．
点评 本题主要考查多边形的内角和定理，解题的关键是根据已知等量关系列出方程从而解决问题．解题时注意：多边形内角和=（n-2）•180°．
练习册系列答案
相关题目
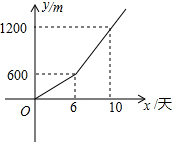（1）在学习一次函数的图象时，我们根据函数图象的定义，按画函数图象的基本步骤，画出一次函数的图象，请您按画函数图象的基本步骤画出函数y=2x+4的图象．
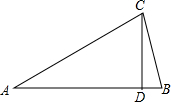如图，在∠A=30°的等腰三角形ABC中，AB=AC，若过点C作CD⊥AB于点D，则∠BCD=15°．根据图形，计算tan15°的值．
5．将一个无盖正方体纸盒展开，展开图不可能是（ ）
| A． |  | B． |  | C． |  | D． |  |
15．下列等式是一元一次方程的是（ ）
| A． | x2+3x=6 | B． | 2x=4 | C． | -$\frac{1}{2}$x-y=0 |
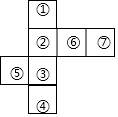小刚在纸上画了一个长方体的展开图，展开图由长方形和正方形构成，淘气的小明在图上又添加了一个四边形，并把这7个面任意标上了①～⑦的序号（如图）．
19．
如图，⊙O的半径为3，正六边形ABCDEF内接于⊙O，则劣弧AC的长为（ ）
如图，⊙O的半径为3，正六边形ABCDEF内接于⊙O，则劣弧AC的长为（ ）| A． | 6π | B． | 3π | C． | 2π | D． | π |