计算20152016=$\sqrt{2}$-1．题目和参考答案——青夏教育精英家教网—

题目内容

20．计算（1+$\sqrt{2}$）²⁰¹⁵（1-$\sqrt{2}$）²⁰¹⁶=$\sqrt{2}$-1．

分析先将（1+$\sqrt{2}$）²⁰¹⁵（1-$\sqrt{2}$）²⁰¹⁶变形为[（1+$\sqrt{2}$）×（1-$\sqrt{2}$）]²⁰¹⁵×（1-$\sqrt{2}$），然后根据二次根式的混合运算的概念和运算法则进行求解即可．

解答解：（1+$\sqrt{2}$）²⁰¹⁵（1-$\sqrt{2}$）²⁰¹⁶
=[（1+$\sqrt{2}$）×（1-$\sqrt{2}$）]²⁰¹⁵×（1-$\sqrt{2}$）
=[-1]²⁰¹⁵×（1-$\sqrt{2}$）
=$\sqrt{2}$-1．
故答案为：$\sqrt{2}$-1．

点评本题考查了二次根式的混合运算，解答本题的关键在于先将（1+$\sqrt{2}$）²⁰¹⁵（1-$\sqrt{2}$）²⁰¹⁶变形为[（1+$\sqrt{2}$）×（1-$\sqrt{2}$）]²⁰¹⁵×（1-$\sqrt{2}$），然后根据二次根式的混合运算的概念和运算法则进行求解．

练习册系列答案

寒假成长乐园系列答案

寒假创新型自主学习第三学期寒假衔接系列答案

相关题目

10．

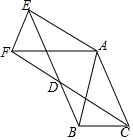△ABC中，AB=AC=1，∠BAC=45°，将△ABC绕点A按顺时针旋转α得到△AEF，连接BE，CF，它们交于D点，
①求证：BE=CF．
②当α=120°，求∠FCB的度数．
③当四边形ACDE是菱形时，求BD的长．

11．

作出图中的三角形关于y轴的轴对称图形，并写出点A关于y轴对称的点的坐标．

8．

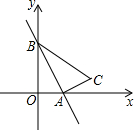已知：如图，一次函数y=-$\sqrt{3}$x+3的图象与x轴、y轴分别交于点A、B，以线段AB为直角边作Rt△ABC，且∠ABC=30°，∠BAC=90°，点C在第一象限
（1）求AB的长及点C的坐标；
（2）求点C作AB的平行线，与x轴、y轴分别相交于点D、E
①求直线DE的解析式；
②若点P是线段DE上的一个点，且△ABP是等腰三角形，求EP的长．

15．当x=2时，代数式ax³+bx+1的值为6，那么当x=-2时，这个代数式的值是（　　）

5．

某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车分别从A、B同时同向出发，沿轨道到达C处停止，甲的速度是乙的速度的2倍，设t（分）后甲、乙两遥控车与B处的距离分别为y₁（米）、y₂（米），且y₁、y₂与t的函数关系如图，试根据图象解决下列问题：
（1）AB的距离为80米，乙遥控车的速度为40米/分，a=1，b=4；（直接填空）
（2）直接写出甲遥控车与B处的距离y₁与时间t的函数关系式；
（3）若甲、乙两遥控车的距离在20米内（含20米）时信号互相干扰，直接写出两遥控车信号互相干扰时t的取值范围．

12．

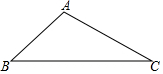如图，BC=50，∠ABC=45°，∠ACB=30°，求点A到BC的距离．

9．（1）已知多项式A=2x²-xy+my-8，B=-nx²+xy+y+7，A-2B中不含有x²项和y项，求n^m+mn的值．
（2）如图，已知线段AB=20，C是AB上的一点，D为CB上的一点，E为DB的中点，DE=3．

①若CE=8，求AC的长；
②若C是AB的中点，求CD的长．

10．一个多边形内角和比四边形的内角和多540度，多边形内角和相等，多边形有几个边（　　）

试题分类