题目内容

19．如图，⊙O的半径为3，正六边形ABCDEF内接于⊙O，则劣弧AC的长为（　　）
A．6πB．3πC．2πD．π

分析 求出圆心角∠AOC的度数，再利用弧长公式解答即可．

解答 解：如图所示：∵ABCDEF为正六边形，
∴∠AOB=360°×$\frac{1}{6}$=60°，
∴∠AOC=120°，
∴$\widehat{AC}$的长为$\frac{120×π×3}{180}$=2π．
故选：C．

点评 此题主要考查了正多边形和圆以及弧长计算，此题将扇形的弧长公式与多边形的性质相结合，构思巧妙，利用了正六边形的性质．

练习册系列答案
相关题目
9．（1）已知多项式A=2x2-xy+my-8，B=-nx2+xy+y+7，A-2B中不含有x2项和y项，求nm+mn的值．
（2）如图，已知线段AB=20，C是AB上的一点，D为CB上的一点，E为DB的中点，DE=3．

①若CE=8，求AC的长；
②若C是AB的中点，求CD的长．
10．一个多边形内角和比四边形的内角和多540度，多边形内角和相等，多边形有几个边（　　）
A．6B．7C．8D．9
7．若x2+4y2+2x-4y+2=0，求5x2+16y2的算术平方根．
14．以下数值反映数据的波动性特征的是（　　）
A．均值B．众数C．方差D．中位数
4．已知抛物线y=3（x-2）2+k（k为常数），A（-3，y1），B（3，y2），C（4，y3）是抛物线上三点，则y1，y2，y3由小到大依序排列为（　　）
A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y1
11．下列点中，一定在二次函数y=x2-1图象上的是（　　）
A．（0，0）B．（1，1）C．（1，0）D．（0，1）
8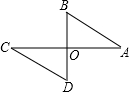．如图，已知AC⊥BD，垂足为O，AO=CO，AB=CD，则可得到△AOB≌△COD，理由是（　　）
A．HLB．SASC．ASAD．AAS
9．下列方程中解为x=-2的是（　　）
A．3x-2=2xB．4x-1=3C．2x+1=x-1D．x-4=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网