题目内容
13.计算:(1)$\frac{2y}{x-1}$+$\frac{3y}{1-x}$-$\frac{y}{1-x}$;
(2)$\frac{y}{{x}^{2}-xy}$+$\frac{x}{{y}^{2}-xy}$;
(3)($\sqrt{2}-\sqrt{3}$)0-($\frac{1}{2}$)-1+$\sqrt{4}$;
(4)(-$\frac{1}{2}$)4÷(-2)-3÷2-2.
分析 (1)(2)通分计算;
(3)先算0指数幂、负整数指数幂、化简二次根式,再算加减;
(4)先算乘方,负指数幂,再算除法.
解答 解:(1)原式=$\frac{2y}{x-1}$-$\frac{3y}{x-1}$+$\frac{y}{x-1}$
=0;
(2)原式=$\frac{{y}^{2}}{xy(x-y)}$-$\frac{{x}^{2}}{xy(x-y)}$
=$\frac{(y-x)(y+x)}{xy(x-y)}$
=-$\frac{x+y}{xy}$;
(3)原式=1-2+2
=1;
(4)原式=$\frac{1}{16}$÷(-$\frac{1}{8}$)÷$\frac{1}{4}$
=$\frac{1}{16}$×(-8)×4
=-2.
点评 此题考查分式的混合运算,掌握分式的性质与运算方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
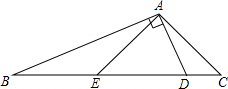 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.若BD=13,则AC=6.5.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.若BD=13,则AC=6.5.