题目内容
8．
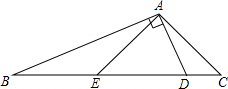如图，在△ABC中，∠C=2∠B，D是BC上的一点，且AD⊥AB，点E是BD的中点，连结AE．若BD=13，则AC=6.5．
分析 根据直角三角形斜边上的中线等于斜边的一半可得AE=BE=ED=$\frac{1}{2}$DB=6.5，再证明AE=AC即可．
解答 解：∵AD⊥AB，点E是BD的中点，
∴AE=BE=ED=$\frac{1}{2}$DB=6.5，
∴∠B=∠BAE，
∴∠AED=2∠B，
∵∠C=2∠B，
∴∠AEC=∠C，
∴AC=AE=6.5．
故答案为：6.5．
点评 此题主要考查了直角三角形的性质，以及等腰三角形的判定，关键是掌握在直角三角形中，斜边上的中线等于斜边的一半．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
18．关于x的一元二次方程（m-2）2x2+（2m+1）x+1=0有两个不相等的实数根，则m的取值范围是（ ）
| A． | m＜2 | B． | m＞$\frac{5}{4}$且m≠2 | C． | m≤2 | D． | m≥$\frac{5}{4}$且m≠2 |